题目内容
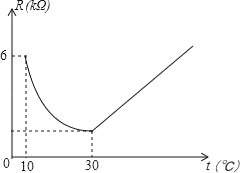
【题目】甲、乙两人驾车都从Р地出发，沿一条笔直的公路匀速前往Q地，乙先出发一段时间后甲再出发，甲、乙两人到达Q地后均停止，已知P、Q两地相距200 km，设乙行驶的时间为t（h），甲、乙两人之间的距离为y（km），表示y与t函数关系的部分图象如图所示．请解决以下问题：
（1）由图象可知，甲比乙迟出发________h．图中线段BC所在直线的函数解析式为________________；
（2）设甲的速度为
，求出
的值；
（3）根据题目信息补全函数图象（不需要写出分析过程，但必须标明关键点的坐标）；并直接写出当甲、乙两人相距32 km时t的值．
【答案】（1）1；
；（2）；
；（3）图象见解析，4.8
【解析】
（1）观察图象可知乙在点A时甲才出发得出甲比乙迟出发
，然后设线段BC所在直线的函数解析式为
代入B、C的坐标求的解析式即可；
（2）设乙的速度为
，根据时间×速度=距离，列出方程组求解即可；
（3）根据（2）求得的速度，算出甲没出发前甲乙的距离、乙到达终点时甲乙相距最远的时间和距离、乙最后到达终点使用的时间，把这些数据不全到途中，乙出发1小时后甲出发，此时甲乙相距
，所以判断只有在乙超过甲后才可能出现甲、乙两人相距32 km，据此列出方程求解即可.
解：（1）观察图象可知乙在点A时甲才出发，
∴甲比乙迟出发；
设线段BC所在直线的函数解析式为
代入点
得：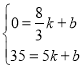
解得：
∴线段BC所在直线的函数解析式为：
；
（2）设乙的速度为，
由题意得：
，
解得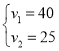
，
∴
；
（3）根据（2）可知甲的速度为
，乙的速度为
∴甲没出发前，乙开了
∴总共用时为：
当甲到达终点时甲乙两人相距最远，
此时甲乙两人相距最远的距离为：
将上面的数据标记到图上，如下图所示：
由（1）可知乙出发1小时后甲出发，此时甲乙相距
∵乙的速度比甲快
∴只能是乙超过甲后才可能出现甲、乙两人相距32 km
∴
解得
