题目内容
【题目】如图,在矩形纸片ABCD中,已知AB=1,BC= ![]() ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.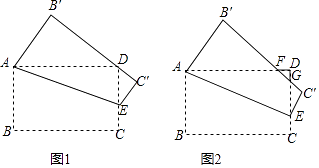
(1)当B′C′恰好经过点D时(如图1),求线段CE的长;
(2)若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°(如图2),求△DFG的面积;
(3)在点E从点C移动到点D的过程中,求点C′运动的路径长.
【答案】
(1)
解:如图1中,设CE=EC′=x,则DE=1﹣x,
∵∠ADB′+∠EDC′=90°,∠B′AD+∠ADB′=90°,
∴∠B′AD=∠EDC′,
∵∠B′=∠C′=90°,AB′=AB=1,AD= ![]() ,
,
∴DB′= ![]() =
= ![]() ,
,
∴△ADB′′∽△DEC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴x= ![]() ﹣2.
﹣2.
∴CE= ![]() ﹣2.
﹣2.
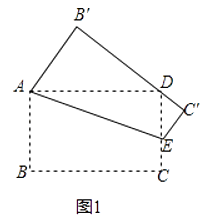
(2)
解:如图2中,
∵∠BAD=∠B′=∠D=90°,∠DAE=22.5°,
∴∠EAB=∠EAB′=67.5°,
∴∠B′AF=∠B′FA=45°,
∴∠DFG=∠AFB′=∠DGF=45°,
∴DF=FG,
在Rt△AB′F中,AB′=FB′=1,
∴AF= ![]() AB′=
AB′= ![]() ,
,
∴DF=DG= ![]() ﹣
﹣ ![]() ,
,
∴S△DFG= ![]() (
( ![]() ﹣
﹣ ![]() )2=
)2= ![]() ﹣
﹣ ![]()

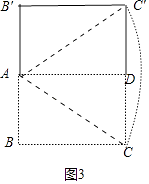
(3)
解:如图3中,点C的运动路径的长为 ![]() 的长,
的长,
在Rt△ADC中,∵tan∠DAC= ![]() =
= ![]() ,
,
∴∠DAC=30°,AC=2CD=2,
∵∠C′AD=∠DAC=30°,
∴∠CAC′=60°,
∴ ![]() 的长=
的长= ![]() =
= ![]() π.
π.
【解析】(1)如图1中,设CE=EC′=x,则DE=1﹣x,由△ADB′′∽△DEC,可得 ![]() =
= ![]() ,列出方程即可解决问题;(2)如图2中,首先证明△ADB′,△DFG都是等腰直角三角形,求出DF即可解决问题;(3)如图3中,点C的运动路径的长为
,列出方程即可解决问题;(2)如图2中,首先证明△ADB′,△DFG都是等腰直角三角形,求出DF即可解决问题;(3)如图3中,点C的运动路径的长为 ![]() 的长,求出圆心角、半径即可解决问题.
的长,求出圆心角、半径即可解决问题.
【考点精析】根据题目的已知条件,利用等腰直角三角形和圆心角、弧、弦的关系的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?