题目内容
等腰梯形中位线长15cm,一个底角为60°,且一条对角线平分这个角,则这个等腰梯形周长是______cm.
如图,等腰梯形ABCD,中位线EF=15cm,∠B=60°,BD平分∠B,求等腰梯形的周长.
法一:过点D作DG∥AB交BC于点G
∵∠B=60°,BD平分∠B
∴∠ABD=∠ADB=30°
∴AD=AB=DC
∵AD∥BC,AB∥DG
∴AD=BG,△DGC为等边三角形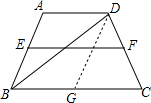
∴CG=CD
∴BC=2AD
∵EF=15cm
∴AD+BC=3AD=30cm
∴AD=10cm,BC=20cm
∴等腰梯形的周长=10+10+20+10=50cm;
法二:∵∠C=∠ABC=60°,BD平分∠ABC,
∴∠DBC=30°,
∴∠BDC=180°-30°-60°=90°,
∴Rt△BCD中,DC=
BC,
∵AD∥BC,
∴∠ADB=∠DBC,
∵∠ABD=∠DBC,
∴AB=AD,
即AD=AB=DC,
∵BC=2DC=2AD,
∴AD+2AD=30,
即AD=10cm,
∴等腰梯形的周长=10+10+10+20=50cm.
法一:过点D作DG∥AB交BC于点G
∵∠B=60°,BD平分∠B
∴∠ABD=∠ADB=30°
∴AD=AB=DC
∵AD∥BC,AB∥DG
∴AD=BG,△DGC为等边三角形

∴CG=CD
∴BC=2AD
∵EF=15cm
∴AD+BC=3AD=30cm
∴AD=10cm,BC=20cm
∴等腰梯形的周长=10+10+20+10=50cm;
法二:∵∠C=∠ABC=60°,BD平分∠ABC,
∴∠DBC=30°,
∴∠BDC=180°-30°-60°=90°,
∴Rt△BCD中,DC=
| 1 |
| 2 |
∵AD∥BC,
∴∠ADB=∠DBC,
∵∠ABD=∠DBC,
∴AB=AD,
即AD=AB=DC,
∵BC=2DC=2AD,
∴AD+2AD=30,
即AD=10cm,
∴等腰梯形的周长=10+10+10+20=50cm.

练习册系列答案
相关题目


 之停止运动,设运动的时间为t秒.
之停止运动,设运动的时间为t秒.


