题目内容
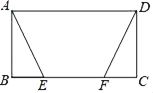
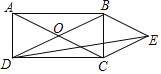
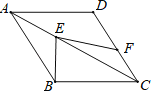
【题目】如图,在菱形ABCD中,点E在对角线AC上,点F在边CD上,连接BE、EF.若∠EFC=90°+![]() ∠CBE,BE=7,EF=10.则点D到EF的距离为_____.
∠CBE,BE=7,EF=10.则点D到EF的距离为_____.
【答案】2![]()
【解析】
连接DE,过D作DG⊥EF于G,由菱形的性质得到AB=AD,∠BAE=∠DAE,从而证得△ABE≌△ADE,进而求得∠CBE=∠CDE,然后结合题目条件和等量代换求得∠EDG=![]() ∠CDE=∠FDG,进而用ASA定理证明△EDG≌△FDG,得到ED=DF,BE=DF=7,GE=
∠CDE=∠FDG,进而用ASA定理证明△EDG≌△FDG,得到ED=DF,BE=DF=7,GE=![]() EF=5,然后利用勾股定理求解即可得到结论.
EF=5,然后利用勾股定理求解即可得到结论.
解:连接DE,过D作DG⊥EF于G,则∠DEF+∠EDG=90°,
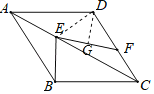
∵四边形ABCD是菱形,
∴AB=AD,∠BAE=∠DAE,
∵AE=AE,
∴△ABE≌△ADE(SAS),
∴BE=DE,∠ABE=∠ADE,
∵∠ABC=∠ADC,
∴∠CBE=∠CDE,
∵∠EFC=∠CDE+∠DEF,∠EFC=90°+![]() ∠CBE,
∠CBE,
∴90°+![]() ∠CBE=∠CDE+∠DEF,
∠CBE=∠CDE+∠DEF,
∴![]() ∠CDE+∠DEF=90°,
∠CDE+∠DEF=90°,
∴∠EDG=![]() ∠CDE=∠FDG,
∠CDE=∠FDG,
∵DG=DG,∠DGE=∠DGF=90°,
∴△EDG≌△FDG(ASA),
∴ED=DF,
∴BE=DF=7,
∴GE=![]() EF=5,
EF=5,
∴在Rt△DGE中,DG=![]() ,
,
∴点D到EF的距离为2![]() ,
,
故答案为:2![]() .
.

【题目】去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩( | 频数(人数) |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
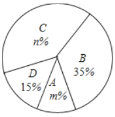
根据以上信息,解答以下问题:
(1)表中的![]() ;
;
(2)扇形统计图中![]() ,
,![]() ,
,![]() 等级对应的扇形的圆心角为 度;
等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得![]() 等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用
等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用![]() ,
,![]() ,
,![]() 表示)和3名女生(用
表示)和3名女生(用![]() ,
,![]() ,
,![]() 表示),请用列表或画树状图的方法求恰好选取的是
表示),请用列表或画树状图的方法求恰好选取的是![]() 和
和![]() 的概率.
的概率.