��Ŀ����
����Ŀ�����ϣ�һ��أ�n����ͬ������a��ˣ� 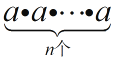 ��Ϊan ��
��Ϊan ��
��23=8����ʱ��3������2Ϊ��8�Ķ�������Ϊlog28����log28=3����
һ��أ���an=b��a��0��a��1��b��0������n������aΪ��b�Ķ�������Ϊlogab����logab=n������34=81����4������3Ϊ��81�Ķ�������Ϊlog381����log381=4����
���⣺
��1��log24��log216��log264֮������ĵ�����ϵ����
��2���²���ۣ�logaM+logaN=��a��0��a��1��M��0��N��0��
��3�������ݵ����㷨��anam=an+m�Լ������ĺ���˵����2������ó��Ľ��ۣ�
���𰸡�
��1��log24+log216=log264
��2��logaMN
��3��
�⣺��x=logaM��y=logaN��
���ݶ����ĺ��壺ax=M��ay=N��
�����ݵ����㷨��MN=axay=ax+y��
���ݶ����ĺ��壺x+y=logaMN��
��logaM+logaN=x+y=logaMN.
����������1��log24=2��log216=4��log264=6����log24+log216=log264����2���ɣ�1�����У�log24+log216=log2��4��16��=log264���ɲ²�logaM+logaN=x+y=logaMN.
�����㾫�����������⣬������Ҫ�˽�����ʽ�Ĺ���(�ȴ�ͼ����Ѱ�ҹ��ɣ�Ȼ����֤���ɣ�Ӧ�ù��ɣ������ν��Ѱ�ҹ���)����Ҫ����ͬ�����ݵij˷�(ͬ�����ݵij˷�����aman=am+n(m,n��������))�����֪ʶ���Ǵ���Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�