题目内容
 如图,已知:AB=
如图,已知:AB= ,BC=2,CD=1,∠ABC=45°,则四边形ABCD的面积为
,BC=2,CD=1,∠ABC=45°,则四边形ABCD的面积为
- A.
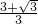
- B.
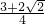
- C.
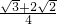
- D.
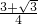
D
分析:如图,连接AC、OD,OD与AC交于点E.BC是直径,则∠BAC=90°,而∠ABC=45°,由此可以推出△ABC,△AOC是等腰直角三角形,AC=AB= ,而BC=2,∴AO=OD=OB=1,∵CD=1,由此推出△OCD是等边三角形,∠DOC=60°,∠AOD=30°,再根据S四边形ABCD=S△ABO+S△ODC+S△AOD即可取出面积.
,而BC=2,∴AO=OD=OB=1,∵CD=1,由此推出△OCD是等边三角形,∠DOC=60°,∠AOD=30°,再根据S四边形ABCD=S△ABO+S△ODC+S△AOD即可取出面积.
解答: 解:如图,连接AC、OD,OD与AC交于点E.BC是直径,
解:如图,连接AC、OD,OD与AC交于点E.BC是直径,
则∠BAC=90°,
∵∠ABC=45°,
∴△ABC,△AOC是等腰直角三角形,AC=AB= ,
,
∵BC=2,
∴AO=OD=OB=1.
∵CD=1,
∴△OCD是等边三角形,
∠DOC=60°,∠AOD=30°
∴S四边形ABCD=S△ABO+S△ODC+S△AOD
= OB•OA+
OB•OA+ OC•ODsin60°+
OC•ODsin60°+ OA•ODsin30°
OA•ODsin30°
= +
+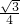 +
+
=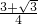 .
.
故选D.
点评:本题考查了垂径定理,等腰直角三角形的判定和性质,等边三角形的判定和性质,三角形的面积公式求解,综合性比较强.
分析:如图,连接AC、OD,OD与AC交于点E.BC是直径,则∠BAC=90°,而∠ABC=45°,由此可以推出△ABC,△AOC是等腰直角三角形,AC=AB=
 ,而BC=2,∴AO=OD=OB=1,∵CD=1,由此推出△OCD是等边三角形,∠DOC=60°,∠AOD=30°,再根据S四边形ABCD=S△ABO+S△ODC+S△AOD即可取出面积.
,而BC=2,∴AO=OD=OB=1,∵CD=1,由此推出△OCD是等边三角形,∠DOC=60°,∠AOD=30°,再根据S四边形ABCD=S△ABO+S△ODC+S△AOD即可取出面积.解答:
 解:如图,连接AC、OD,OD与AC交于点E.BC是直径,
解:如图,连接AC、OD,OD与AC交于点E.BC是直径,则∠BAC=90°,
∵∠ABC=45°,
∴△ABC,△AOC是等腰直角三角形,AC=AB=
 ,
,∵BC=2,
∴AO=OD=OB=1.
∵CD=1,
∴△OCD是等边三角形,
∠DOC=60°,∠AOD=30°
∴S四边形ABCD=S△ABO+S△ODC+S△AOD
=
 OB•OA+
OB•OA+ OC•ODsin60°+
OC•ODsin60°+ OA•ODsin30°
OA•ODsin30°=
 +
+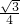 +
+
=
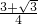 .
.故选D.
点评:本题考查了垂径定理,等腰直角三角形的判定和性质,等边三角形的判定和性质,三角形的面积公式求解,综合性比较强.

练习册系列答案
相关题目
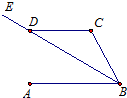 13、如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为
13、如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为
 (2013•温州一模)如图,已知线段AB,
(2013•温州一模)如图,已知线段AB,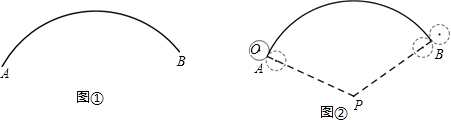
 如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.
如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.