题目内容
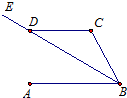 13、如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为
13、如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为
120
.分析:先根据平行线及角平分线的性质求出∠CDB=∠CBD,再根据平角的性质求出∠CDB的度数,再根据平行线的性质求出∠C的度数即可.
解答:解:∵直线AB∥CD,
∴∠CDB=∠ABD,
∵∠CDB=180°-∠CDE=30°,
∴∠ABD=30°,
∵BE平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABC=∠CBD+∠ABD=60°,
∵AB∥CD,
∴∠C=180°-∠ABC=180°-60°=120°,
故答案为120°.
∴∠CDB=∠ABD,
∵∠CDB=180°-∠CDE=30°,
∴∠ABD=30°,
∵BE平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABC=∠CBD+∠ABD=60°,
∵AB∥CD,
∴∠C=180°-∠ABC=180°-60°=120°,
故答案为120°.
点评:本题考查的是平行线、平角的定义以及角平分线的性质,比较简单.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
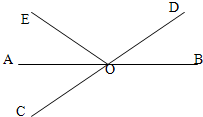 13、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于
13、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于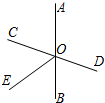 15、如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=50°,那么∠AOC=
15、如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=50°,那么∠AOC=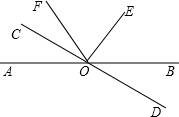 如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.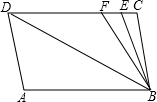 如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.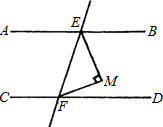 如图,已知直线AB∥CD,EM⊥FM,∠MFD=25°,求∠MEB的度数.
如图,已知直线AB∥CD,EM⊥FM,∠MFD=25°,求∠MEB的度数.