题目内容
 (2013•温州一模)如图,已知线段AB,
(2013•温州一模)如图,已知线段AB,(1)线段AB为腰作一个黄金三角形(尺规作图,要求保留作图痕迹,不必写出作法);
(友情提示:三角形两边之比为黄金比的等腰三角形叫做黄金三角形)
(2)若AB=2,求出你所作的黄金三角形的周长.
分析:(1)根据底与腰之比均为黄金比的等腰三角形以及腰与底之比为黄金比为黄金比分别求出即可;
(2)利用黄金比为
,求出三角形底边长即可得出答案.
(2)利用黄金比为
| ||
| 2 |
解答: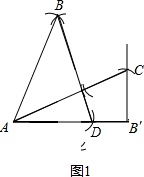 解:(1)可分为两种情况:底与腰之比均为黄金比的等腰三角形如图1,腰与底之比为黄金比为黄金比如图2,
解:(1)可分为两种情况:底与腰之比均为黄金比的等腰三角形如图1,腰与底之比为黄金比为黄金比如图2,
(2)∵如图1,AB=2,当底与腰之比为黄金比时:
∴
=
,
∴AD=
-1,
∴AB+AD+BD=
+3,
如图2,当腰与底之比为黄金比时,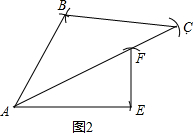
=
,
∴AC=
+1,
∴△ABC周长为5+
.
 解:(1)可分为两种情况:底与腰之比均为黄金比的等腰三角形如图1,腰与底之比为黄金比为黄金比如图2,
解:(1)可分为两种情况:底与腰之比均为黄金比的等腰三角形如图1,腰与底之比为黄金比为黄金比如图2,(2)∵如图1,AB=2,当底与腰之比为黄金比时:
∴
| AD |
| AB |
| ||
| 2 |
∴AD=
| 5 |
∴AB+AD+BD=
| 5 |
如图2,当腰与底之比为黄金比时,

| AB |
| AC |
| ||
| 2 |
∴AC=
| 5 |
∴△ABC周长为5+
| 5 |
点评:此题主要考查了黄金三角形的作法以及黄金三角形的性质,根据已知得出底边作法是解题关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目