题目内容
 一次函数y=kx+k的图象经过点(1,4),且分别与x轴、y轴交于点A、B.点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB.
一次函数y=kx+k的图象经过点(1,4),且分别与x轴、y轴交于点A、B.点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB.
(1)求k的值,并在给出的平面直角坐标系中画出该一次函数的图象;
(2)求a与b满足的等量关系式.
 解:(1)一次函数y=kx+k的图象经过点(1,4),
解:(1)一次函数y=kx+k的图象经过点(1,4),则 4=k+k,k=2,
∴y=2x+2.
该函数的图象见图:
(2)函数y=2x+2的图象与x轴、y轴的交点分别为A(-1,0)、B(0,2),
∵PQ⊥AB,设交点为M,
则∠ABO=∠MBQ=∠QPO,∠AOB=∠QOP=90°
∴△AOB∽△QOP,
∴
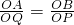 ,即
,即 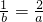
∴a=2b.
分析:(1)本题须把(1,4)代入y=kx+k先求出一次函数的解析式,再画出函数图象即可.
(2)本题须先求出函数y=2x+2的图象与x轴、y轴的交点,再证出△AOB∽△QOP,即可得出
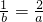 ,从而证出a=2b.
,从而证出a=2b.点评:本题主要考查了一次函数的综合应用,在解题时要注意与相似三角形的判定和性质相结合是本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
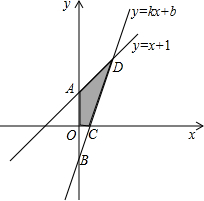 x轴以及y=x+1的图象分别交于点C、D.
x轴以及y=x+1的图象分别交于点C、D. 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y=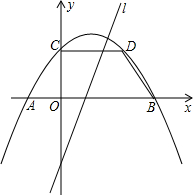 (2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,