题目内容
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与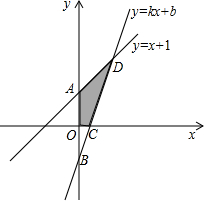 x轴以及y=x+1的图象分别交于点C、D.
x轴以及y=x+1的图象分别交于点C、D.(1)若点D的横坐标为1,求四边形AOCD的面积(即图中阴影部分的面积);
(2)在第(1)小题的条件下,在y轴上是否存在这样的点P,使得以点P、B、D为顶点的三角形是等腰三角形.如果存在,求出点P坐标;如果不存在,说明理由.
(3)若一次函数y=kx+b的图象与函数y=x+1的图象的交点D始终在第一象限,则系数k的取值范围是
分析:(1)先求出点D的坐标,再求出BD的解析式,然后根据S四边形AOCD=S△AOD+S△COD即可求解;
(2)分三种情况讨论:①当DP=DB时,②当BP=DB时,③当PB=PD时;
(3)根据图象即可得出答案.
(2)分三种情况讨论:①当DP=DB时,②当BP=DB时,③当PB=PD时;
(3)根据图象即可得出答案.
解答:解:(1)∵点D的横坐标为1,点D在y=x+1的图象上,∴D(1,2),
∴直线BD的解析式为y=3x-1,∴A(0,1),C(
,0),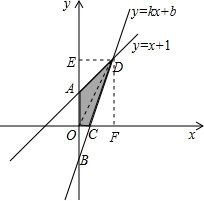
∴S四边形AOCD=S△AOD+S△COD=
×1×1+
×
×2=
;
(2)①当DP=DB时,设P(0,y),
∵B(0,-1),D(1,2),
∴DP2=12+(y-2)2=DB2=12+(2+1)2,
∴P(0,5);
②当BP=DB时,DB=
,∴P(0,-1-
)或P(0,
-1);
③当PB=PD时,设P(0,a),则(a+1)2=1+(2-a)2,解得a=
,
∴P(0,
);
(3)若一次函数y=kx+b的图象与函数y=x+1的图象的交点D始终在第一象限,则系数k的取值范围是:k>1.
∴直线BD的解析式为y=3x-1,∴A(0,1),C(
| 1 |
| 3 |

∴S四边形AOCD=S△AOD+S△COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
(2)①当DP=DB时,设P(0,y),
∵B(0,-1),D(1,2),
∴DP2=12+(y-2)2=DB2=12+(2+1)2,
∴P(0,5);
②当BP=DB时,DB=
| 10 |
| 10 |
| 10 |
③当PB=PD时,设P(0,a),则(a+1)2=1+(2-a)2,解得a=
| 2 |
| 3 |
∴P(0,
| 2 |
| 3 |
(3)若一次函数y=kx+b的图象与函数y=x+1的图象的交点D始终在第一象限,则系数k的取值范围是:k>1.
点评:本题考查了一次函数综合知识,难度适中,关键是掌握分类讨论思想的运用.

练习册系列答案
相关题目
 如图,已知函数y1=kx+b与函数y2=
如图,已知函数y1=kx+b与函数y2=| m |
| x |
| m |
| x |
| A、x1=1,x2=-3 |
| B、x1=-1,x2=3 |
| C、x1=1,x2=-1 |
| D、x1=3,x2=-3 |
 14、如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集在数轴上表示正确的是( )
14、如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集在数轴上表示正确的是( ) 12、如图,已知函数y=x+b和y=ax+3的图象交点为P,则不等式x+b>ax+3的解集为
12、如图,已知函数y=x+b和y=ax+3的图象交点为P,则不等式x+b>ax+3的解集为
 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于 如图,已知函数
如图,已知函数