��Ŀ����
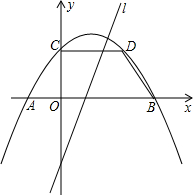 ��2013•Ϋ������ͼ��������y=ax2+bx+c����ֱ��x=1�Գƣ��������ύ��A��B��C���㣬��AB=4����D��2��
��2013•Ϋ������ͼ��������y=ax2+bx+c����ֱ��x=1�Գƣ��������ύ��A��B��C���㣬��AB=4����D��2��| 3 | 2 |
��1���������ߵĽ���ʽ��
��2����ֱ��lƽ���ı���OBDC���������k��ֵ��
��3��������������ƽ��1����λ��������ƽ��2����λ��������������ֱ��l����M��N���㣬����y�����������Ƿ����һ����P��ʹ�ò���kȡ��ֵ��ֱ��PM��PN���ǹ���y��Գƣ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
��������1�����������A��B�����꣬Ȼ�����ý���ʽ������ϵ������������ߵĽ���ʽ��
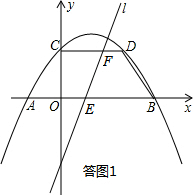
��2�����������C���꣬ȷ��CD��OB�������⣬ֱ��lƽ���ı���OBDC���������S����OEFC=S����FDBE���ݴ��з������k��ֵ��
��3���������ƽ�Ʊ任��������߽���ʽ�����ͼ2��ʾ��Ȼ��֤��Rt��PMD��Rt��PNE�������������α����߶ι�ϵ�õ�ʽ�٣�
=
������֮���Ϊʽ�ڣ���t+2����xm+xn��=2kxmxn���������һԪ���η��̸���ϵ���Ĺ�ϵ���t��ֵ��
��2�����������C���꣬ȷ��CD��OB�������⣬ֱ��lƽ���ı���OBDC���������S����OEFC=S����FDBE���ݴ��з������k��ֵ��
��3���������ƽ�Ʊ任��������߽���ʽ�����ͼ2��ʾ��Ȼ��֤��Rt��PMD��Rt��PNE�������������α����߶ι�ϵ�õ�ʽ�٣�
| -xm |
| xn |
| t-ym |
| t-yn |
��� �⣺��1����Ϊ�����߹���ֱ��x=1�Գƣ�AB=4������A��-1��0����B��3��0����
�⣺��1����Ϊ�����߹���ֱ��x=1�Գƣ�AB=4������A��-1��0����B��3��0����
�������ߵĽ���ʽΪy=a��x+1����x-3����
�ߵ�D��2��
�����������ϣ�
��
=a��3����-1�������a=-
��
�������߽���ʽΪ��y=-
��x+1����x-3��=-
x2+x+
��
��2�������߽���ʽΪ��y=-
x2+x+
����x=0����y=
����C��0��
����
��D��2��
������CD��OB��ֱ��CD����ʽΪy=
��
ֱ��l����ʽΪy=kx-2����y=0����x=
����y=
����x=
��
���ͼ1��ʾ����ֱ��l�ֱ���OB��CD���ڵ�E��F����E��
��0����F��
��
����
OE=
��BE=3-
��CF=
��DF=2-
��
��ֱ��lƽ���ı���OBDC�������
��S����OEFC=S����FDBE��
��
��OE+CF��•OC=
��FD+BE��•OC��
��OE+CF=FD+BE������
+
=��3-
��+��2-
����
�ⷽ�̵ã�k=
��������k=
��ԭ���̵Ľ��ҷ������⣬
��k=
��
��3��������ڷ�������ĵ�P��������Ϊ��0��t����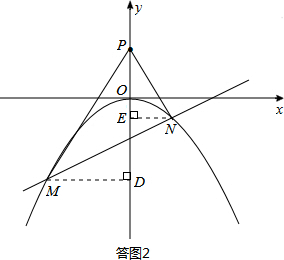
�����߽���ʽΪ��y=-
x2+x+
=-
��x-1��2+2��
������������ƽ��1����λ��������ƽ��2����λ�����������߽���ʽΪ��y=-
x2��
�����⻭��ͼ�Σ����ͼ2��ʾ������M��MD��y���ڵ�D��NE��y���ڵ�E��
��M��xm��ym����N��xn��yn������MD=-xm��PD=t-ym��NE=xn��PE=t-yn��
��ֱ��PM��PN����y��Գƣ����MPD=��NPE��
�֡�MDP=��NEP=90�㣬
��Rt��PMD��Rt��PNE��
��
=
����
=
�٣�
�ߵ�M��N��ֱ��y=kx-2�ϣ���ym=kxm-2��yn=kxn-2��
�����ʽ����ã���t+2����xm+xn��=2kxmxn ��
��y=kx-2����y=-
x2���������ã�x2+2kx-4=0��
��xm+xn=-2k��xmxn=-4�������ʽ��ã�t=2������������
������y���������ϴ���һ������P��0��2����ʹ�ò���kȡ��ֵ��ֱ��PM��PN���ǹ���y��Գƣ�
 �⣺��1����Ϊ�����߹���ֱ��x=1�Գƣ�AB=4������A��-1��0����B��3��0����
�⣺��1����Ϊ�����߹���ֱ��x=1�Գƣ�AB=4������A��-1��0����B��3��0�����������ߵĽ���ʽΪy=a��x+1����x-3����
�ߵ�D��2��
| 3 |
| 2 |
��
| 3 |
| 2 |
| 1 |
| 2 |
�������߽���ʽΪ��y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��2�������߽���ʽΪ��y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
��D��2��
| 3 |
| 2 |
| 3 |
| 2 |
ֱ��l����ʽΪy=kx-2����y=0����x=
| 2 |
| k |
| 3 |
| 2 |
| 7 |
| 2k |
���ͼ1��ʾ����ֱ��l�ֱ���OB��CD���ڵ�E��F����E��
| 2 |
| k |
| 7 |
| 2k |
| 3 |
| 2 |
OE=
| 2 |
| k |
| 2 |
| k |
| 7 |
| 2k |
| 7 |
| 2k |
��ֱ��lƽ���ı���OBDC�������
��S����OEFC=S����FDBE��
��
| 1 |
| 2 |
| 1 |
| 2 |
��OE+CF=FD+BE������
| 2 |
| k |
| 7 |
| 2k |
| 2 |
| k |
| 7 |
| 2k |
�ⷽ�̵ã�k=
| 11 |
| 5 |
| 11 |
| 5 |
��k=
| 11 |
| 5 |
��3��������ڷ�������ĵ�P��������Ϊ��0��t����

�����߽���ʽΪ��y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
������������ƽ��1����λ��������ƽ��2����λ�����������߽���ʽΪ��y=-
| 1 |
| 2 |
�����⻭��ͼ�Σ����ͼ2��ʾ������M��MD��y���ڵ�D��NE��y���ڵ�E��
��M��xm��ym����N��xn��yn������MD=-xm��PD=t-ym��NE=xn��PE=t-yn��
��ֱ��PM��PN����y��Գƣ����MPD=��NPE��
�֡�MDP=��NEP=90�㣬
��Rt��PMD��Rt��PNE��
��
| MD |
| NE |
| PD |
| PE |
| -xm |
| xn |
| t-ym |
| t-yn |
�ߵ�M��N��ֱ��y=kx-2�ϣ���ym=kxm-2��yn=kxn-2��
�����ʽ����ã���t+2����xm+xn��=2kxmxn ��
��y=kx-2����y=-
| 1 |
| 2 |
��xm+xn=-2k��xmxn=-4�������ʽ��ã�t=2������������
������y���������ϴ���һ������P��0��2����ʹ�ò���kȡ��ֵ��ֱ��PM��PN���ǹ���y��Գƣ�
�����������Ƕ��κ����ۺ��⣬�����˶��κ�����ͼ�������ʡ�����ϵ�����������ߵ�ƽ�ơ����������Ρ�һԪ���η��̸���ϵ����ϵ��ͼ����������֪ʶ�㣬��һ�����Ѷȣ��ڣ�2���ʵĽ���Ҫ���Ǹ���S����OEFC=S����FDBE�����ͼ1���з�����⣬�ڣ�3�����Ǵ��������⣬�ۺ��������������ε��ж������ʡ�����ͼ���ϵ������������һԪ���η��̸���ϵ����ϵ��⣮

��ϰ��ϵ�д�
�����Ŀ
 ��2013•Ϋ������ͼ�dz��õ�һ��Բ���ݸˣ����ĸ���ͼ��ȷ���ǣ�������
��2013•Ϋ������ͼ�dz��õ�һ��Բ���ݸˣ����ĸ���ͼ��ȷ���ǣ�������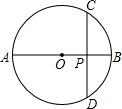 ��2013•Ϋ������ͼ����O��ֱ��AB=12��CD�ǡ�O���ң�CD��AB������ΪP����BP��AP=1��5����CD�ij�Ϊ��������
��2013•Ϋ������ͼ����O��ֱ��AB=12��CD�ǡ�O���ң�CD��AB������ΪP����BP��AP=1��5����CD�ij�Ϊ��������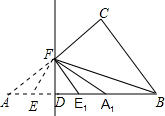 ��2013•Ϋ������ͼ��ֱ��������ABC�У���ACB=90�㣬AB=10��BC=6�����߶�AB��ȡһ��D����DF��AB��AC�ڵ�F���ֽ���ADF��DF�۵���ʹ��A�����߶�DB�ϣ���Ӧ���ΪA1��AD���е�E�Ķ�Ӧ���ΪE1������E1FA1�ס�E1BF����AD=
��2013•Ϋ������ͼ��ֱ��������ABC�У���ACB=90�㣬AB=10��BC=6�����߶�AB��ȡһ��D����DF��AB��AC�ڵ�F���ֽ���ADF��DF�۵���ʹ��A�����߶�DB�ϣ���Ӧ���ΪA1��AD���е�E�Ķ�Ӧ���ΪE1������E1FA1�ס�E1BF����AD=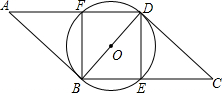 ��2013•Ϋ������ͼ���ı���ABCD��ƽ���ı��Σ��ԶԽ���BDΪֱ������O���ֱ���BC��AD�ཻ�ڵ�E��F��
��2013•Ϋ������ͼ���ı���ABCD��ƽ���ı��Σ��ԶԽ���BDΪֱ������O���ֱ���BC��AD�ཻ�ڵ�E��F��