题目内容
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
(1)求⊙M的半径.
(2)求线段AC的长.
(3)若D为OA的中点,求证:CD是⊙M的切线.

(1)求⊙M的半径.
(2)求线段AC的长.
(3)若D为OA的中点,求证:CD是⊙M的切线.

(1)∵OA=4∴A(4,0)
又OA•OB长是x2-mx+12=0的两根
∴OA•OB=12∴OB=3故B(0,3)(2分)
∵OB为直径
∴半径MB=
(4分)
(2)连接OC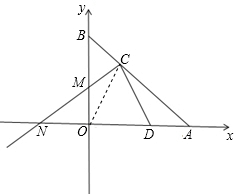
∵OB是⊙M直径
∴OC⊥BC(5分)
∴OC•AB=OA•OB
∵AB=
=5(6分)
∴OC•5=3•4
∴OC=
(7分)
∴AC=
=
(8分)
(3)∵OM=MC∴∠MOC=∠MCO(9分)
又CD是Rt△OCA斜边上中线
∴DC=DO
∴∠DOC=∠DCO(10分)
∵∠DOC+∠MOC=90°
∴∠MCO+∠DCO=90°
∴DC⊥MC(11分)
∴CD是⊙M的切线(12分)
(注:由于解法不一,可以视方法的异同与合理性分步计分)
又OA•OB长是x2-mx+12=0的两根
∴OA•OB=12∴OB=3故B(0,3)(2分)
∵OB为直径
∴半径MB=
| 3 |
| 2 |
(2)连接OC

∵OB是⊙M直径
∴OC⊥BC(5分)
∴OC•AB=OA•OB
∵AB=
| 42+32 |
∴OC•5=3•4
∴OC=
| 12 |
| 5 |
∴AC=
42-(
|
| 16 |
| 5 |
(3)∵OM=MC∴∠MOC=∠MCO(9分)
又CD是Rt△OCA斜边上中线
∴DC=DO
∴∠DOC=∠DCO(10分)
∵∠DOC+∠MOC=90°
∴∠MCO+∠DCO=90°
∴DC⊥MC(11分)
∴CD是⊙M的切线(12分)
(注:由于解法不一,可以视方法的异同与合理性分步计分)

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目

 -3),AC交x轴于点N,BC交y轴于点M,
-3),AC交x轴于点N,BC交y轴于点M,
 ,且BE⊥AE,连接AB,
,且BE⊥AE,连接AB, ,并且OC>OE.
,并且OC>OE.
