题目内容
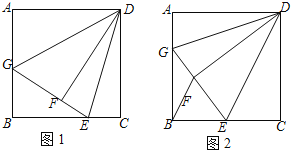
【题目】如图1,在正方形![]() 中,点
中,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠得到
折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求![]() 的度数.
的度数.
(2)如图![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
①求证:![]() ;
;
②若正方形边长为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)![]() ;(2)①详见解析;②
;(2)①详见解析;②![]()
【解析】
(1)由正方形的性质可得DC=DA.∠A=∠B=∠C=∠ADC=90°,由折叠的性质得出∠DFE=∠C,DC=DF,∠1=∠2,再求出∠DFG=∠A,DA=DF,然后由“HL”证明Rt△DGA≌Rt△DGF,由全等三角形对应角相等得出∠3=∠4,得出∠2+∠3=45°即可;
(2)①由折叠的性质和线段中点的定义可得CE=EF=BE,∠DEF=∠DEC,再由三角形的外角性质得出∠5=∠DEC,然后利用同位角相等,两直线平行证明即可;
②设AG=x,表示出GF、BG,根据点E是BC的中点求出BE、EF,从而得到GE的长度,再利用勾股定理列出方程求解即可;
(1)解:如图1所示:

∵四边形ABCD是正方形,
∴DC=DA.∠A=∠B=∠C=∠ADC=90°,
∵△DEC沿DE折叠得到△DEF,
∴∠DFE=∠C,DC=DF,∠1=∠2,
∴∠DFG=∠A=90°,DA=DF,
在Rt△DGA和Rt△DGF中,
![]() ,
,
∴Rt△DGA≌Rt△DGF(HL),
∴∠3=∠4,
∴∠EDG=∠3+∠2=![]() ∠ADF+
∠ADF+![]() ∠FDC=
∠FDC=![]() (∠ADF+∠FDC),
(∠ADF+∠FDC),
=![]() ×90°,
×90°,
=45°;
(2)①证明:如图2所示:

∵△DEC沿DE折叠得到△DEF,E为BC的中点,
∴CE=EF=BE,∠DEF=∠DEC,
∴∠5=∠6,
∵∠FEC=∠5+∠6,
∴∠DEF+∠DEC=∠5+∠6,
∴2∠5=2∠DEC,
即∠5=∠DEC,
∴BF∥DE;
②解:设AG=x,则GF=x,BG=12-x,
∵正方形边长为12,E为BC的中点,
∴CE=EF=BE=![]() ×12=6,
×12=6,
∴GE=EF+GF=6+x,
在Rt△GBE中,根据勾股定理得:(12-x)2+62=(6+x)2,
解得:x=4,
即线段AG的长为4.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案