题目内容
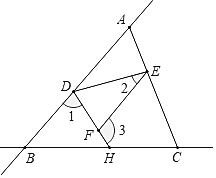
【题目】如图,直线AB和直线BC相交于点B,连接AC,点D、E、H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°.
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=![]() 求∠3的度数(用含
求∠3的度数(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)证明见解析,(2)∠3=90°+![]() α.
α.
【解析】
(1)根据平行线的判定和性质解答即可;
(2)根据平行线的性质解答即可.
解:(1)∵∠3+∠DFE=180°,∠1+∠3=180°
∴∠DFE=∠1,
∴AB∥EF,
∴∠CEF=∠EAD;
(2)∵AB∥EF,
∴∠2+∠BDE=180°
又∵∠2=α
∴∠BDE=180°-α
又∵DH平 分∠BDE
∴∠1=![]() ∠BDE=
∠BDE=![]() (180°-α)
(180°-α)
∴∠3=180°-![]() (180°-α)=90°+
(180°-α)=90°+![]() α
α

练习册系列答案
相关题目