题目内容
如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB = 26m,OE⊥CD于点E.水位正常时测得OE∶CD=5∶24
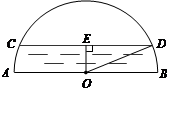
(1)求CD的长;
(2)现汛期来临,水面要以每小时4 m的速度上升,则经过多长时间桥洞会刚刚被灌满?

(1)求CD的长;
(2)现汛期来临,水面要以每小时4 m的速度上升,则经过多长时间桥洞会刚刚被灌满?
(1)24m(2)2小时
解:(1)∵直径AB = 26m
∴OD=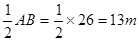 ……………………………………1分
……………………………………1分
∵OE⊥CD
∴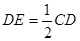 …………………………………………………………..2分
…………………………………………………………..2分
∵OE∶CD=5∶24
∴OE∶ED=5∶12
∴设OE=5x,ED=12x
∴在Rt△ODE中
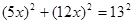 …………………………………………………………4分
…………………………………………………………4分
解得x=1
∴CD=2DE=2×12×1=24m………………………………………….………..5分
(2)由(1)的OE=1×5=5m
延长OE交圆O于点F
∴EF=OF-OE=13-5=8m
∴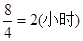 所以经过2小时桥洞会刚刚被灌满………………..…..8分
所以经过2小时桥洞会刚刚被灌满………………..…..8分
(1)利用垂直弦的直径平分这条弦及直角三角形勾股定理求出CD的长度
(2)时间=EF÷4,关键在于求出EF,而EF=OF-OE(OF为半径,OE=5)
∴OD=
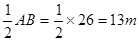 ……………………………………1分
……………………………………1分 ∵OE⊥CD
∴
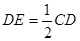 …………………………………………………………..2分
…………………………………………………………..2分 ∵OE∶CD=5∶24
∴OE∶ED=5∶12
∴设OE=5x,ED=12x
∴在Rt△ODE中
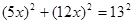 …………………………………………………………4分
…………………………………………………………4分解得x=1
∴CD=2DE=2×12×1=24m………………………………………….………..5分
(2)由(1)的OE=1×5=5m
延长OE交圆O于点F
∴EF=OF-OE=13-5=8m
∴
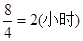 所以经过2小时桥洞会刚刚被灌满………………..…..8分
所以经过2小时桥洞会刚刚被灌满………………..…..8分(1)利用垂直弦的直径平分这条弦及直角三角形勾股定理求出CD的长度
(2)时间=EF÷4,关键在于求出EF,而EF=OF-OE(OF为半径,OE=5)

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
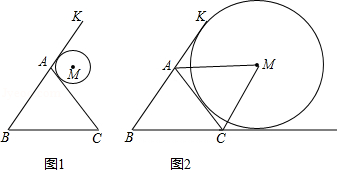

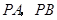 是
是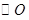 的两条切线,
的两条切线,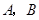 分别为切点,
分别为切点,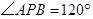 ,
,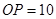 厘米,则弦
厘米,则弦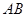 的长为( )
的长为( )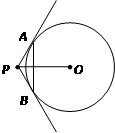
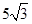 厘米
厘米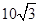 厘米
厘米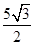 厘米
厘米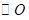 的半径为5,弦
的半径为5,弦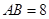 ,
,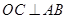 于
于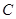 ,则
,则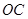 的长等于 .
的长等于 .