题目内容
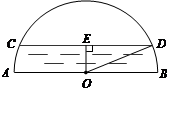
如图,在梯形ABCD中,AB∥CD,∠BAD=90°,以AD为直径的半圆D与BC相切。

(1)求证:OB⊥OC;
(2)若AD=12,∠BCD=60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积。

(1)求证:OB⊥OC;
(2)若AD=12,∠BCD=60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积。
(1)证明见解析(2)4π
(1)∵AB,BC,CD均与半圆O相切,
∴∠ABO=∠CBO,∠DCO=∠BCO.
又AB∥CD,
∴∠ABC+∠BCD=180°,即∠ABO+∠CBO+∠BCO+∠DCO=180°.
∴2∠CBO+2∠BCO=180°,于是∠CBO+∠BCO=90°,
∴∠BOC=180°-(∠CBO+∠BCO)=180°-90°=90°,
即OB⊥OC. ………………………………4分
(2)设CD切⊙O1于点M,连接O1M,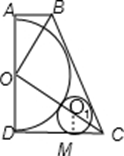
则O1M⊥CD.
设⊙O1的半径为r.
∵∠BCD=60°,且由(1)知∠BCO=∠O1CM,
∴∠O1CM=30°.
在Rt△O1CM中,CO1=2O1M=2r.在Rt△OCD中,OC=2OD=AD=12.
∵⊙O1与半圆D外切,
∴OO1=6+r,于是,由OO1+O1C=OC,即6+r+2r=12,
解得r=2,
因此⊙O1的面积为4π. ………………………………10分
(1)证明两个锐角的和等于90°即可;
(2)求得⊙O1的半径后代入圆的面积公式求得其面积即可.
∴∠ABO=∠CBO,∠DCO=∠BCO.
又AB∥CD,
∴∠ABC+∠BCD=180°,即∠ABO+∠CBO+∠BCO+∠DCO=180°.
∴2∠CBO+2∠BCO=180°,于是∠CBO+∠BCO=90°,
∴∠BOC=180°-(∠CBO+∠BCO)=180°-90°=90°,
即OB⊥OC. ………………………………4分
(2)设CD切⊙O1于点M,连接O1M,

则O1M⊥CD.
设⊙O1的半径为r.
∵∠BCD=60°,且由(1)知∠BCO=∠O1CM,
∴∠O1CM=30°.
在Rt△O1CM中,CO1=2O1M=2r.在Rt△OCD中,OC=2OD=AD=12.
∵⊙O1与半圆D外切,
∴OO1=6+r,于是,由OO1+O1C=OC,即6+r+2r=12,
解得r=2,
因此⊙O1的面积为4π. ………………………………10分
(1)证明两个锐角的和等于90°即可;
(2)求得⊙O1的半径后代入圆的面积公式求得其面积即可.

练习册系列答案
相关题目
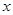 轴相交于点A,与
轴相交于点A,与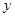 轴相交于点B。
轴相交于点B。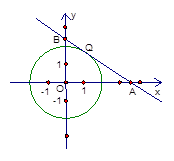
 、
、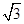 ,则
,则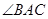 =
=  .
.