题目内容
（2012•宁波模拟）在平面直角坐标系xOy中，已知二次函数y1=ax2+3x+c的图象经过原点及点A（1，2），与x轴相交于另一点B．
（1）求：二次函数y1的解析式及B点坐标；
（2）若将抛物线y1以x=3为对称轴向右翻折后，得到一个新的二次函数y2，已知二次函数y2与x轴交于两点，其中右边的交点为C点．点P在线段OC上，从O点出发向C点运动，过P点作x轴的垂线，交直线AO于D点，以PD为边在PD的右侧作正方形PDEF（当P点运动时，点D、点E、点F也随之运动）；
①当点E在二次函数y1的图象上时，求OP的长．
②若点P从O点出发向C点做匀速运动，速度为每秒1个单位长度，同时线段OC上另一个点Q从C点出发向O点做匀速运动，速度为每秒2个单位长度（当Q点到达O点时停止运动，P点也同时停止运动）．过Q点作x轴的垂线，与直线AC交于G点，以QG为边在QG的左侧作正方形QGMN（当Q点运动时，点G、点M、点N也随之运动），若P点运动t秒时，两个正方形分别有一条边
恰好落在同一条直线上（正方形在x轴上的边除外），求此刻t的值．
（1）求：二次函数y1的解析式及B点坐标；
（2）若将抛物线y1以x=3为对称轴向右翻折后，得到一个新的二次函数y2，已知二次函数y2与x轴交于两点，其中右边的交点为C点．点P在线段OC上，从O点出发向C点运动，过P点作x轴的垂线，交直线AO于D点，以PD为边在PD的右侧作正方形PDEF（当P点运动时，点D、点E、点F也随之运动）；
①当点E在二次函数y1的图象上时，求OP的长．
②若点P从O点出发向C点做匀速运动，速度为每秒1个单位长度，同时线段OC上另一个点Q从C点出发向O点做匀速运动，速度为每秒2个单位长度（当Q点到达O点时停止运动，P点也同时停止运动）．过Q点作x轴的垂线，与直线AC交于G点，以QG为边在QG的左侧作正方形QGMN（当Q点运动时，点G、点M、点N也随之运动），若P点运动t秒时，两个正方形分别有一条边
恰好落在同一条直线上（正方形在x轴上的边除外），求此刻t的值．分析：（1）利用二次函数y1=ax2+3x+c的图象经过原点及点A（1，2），分别代入求出a，c的值即可；
（2）①过A点作AH⊥x轴于H点，根据DP∥AH，得出△OPD∽△OHA，进而求出OP的长；
②分别利用当点F、点N重合时，当点F、点Q重合时，当点P、点N重合时，当点P、点Q重合时，求出t的值即可．
（2）①过A点作AH⊥x轴于H点，根据DP∥AH，得出△OPD∽△OHA，进而求出OP的长；
②分别利用当点F、点N重合时，当点F、点Q重合时，当点P、点N重合时，当点P、点Q重合时，求出t的值即可．
解答：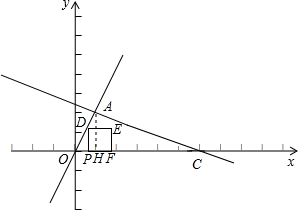
解：（1）∵二次函数y1=ax2+3x+c的图象经过原点及点A（1，2），
∴将（0，0），代入得出：
c=0，
将（1，2）代入得出：
a+3=2，
解得：a=-1，
故二次函数解析式为：y1=-x2+3x，
∵图象与x轴相交于另一点B，
∴0=-x2+3x，
解得：x=0或3，
则B（3，0）；
（2）①由已知可得C（6，0）
如图：过A点作AH⊥x轴于H点，
∵DP∥AH，
∴△OPD∽△OHA，
∴
=
，
即
=
，
∴PD=2a，
∵正方形PDEF，
∴E（3a，2a），
∵E（3a，2a）在二次函数y1=-x2+3x的图象上，
∴a=
；
即OP=
．
②如图1：
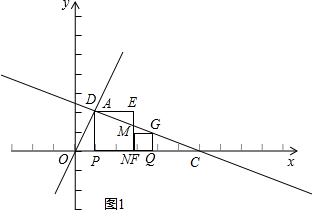
当点F、点N重合时，有OF+CN=6，
∵直线AO过点（1，2），
故直线解析式为：y=2x，
当OP=t，
则AP=2t，
∵直线AC过点（1，2），（6，0），
代入y=ax+b，
，
解得：
，
故直线AC的解析式为：y=-
x+
，
∵当OP=t，QC=2t，
∴QO=6-2t，
∴GQ=-
（6-2t）+
=
t，
即NQ=
t，
∴OP+PN+NQ+QC=6，
则有3t+2t+
t=6，
解得：t=
；
如图2：
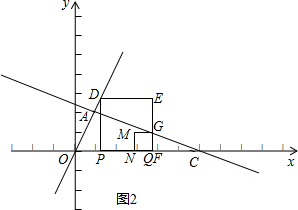
当点F、点Q重合时，有OF+CQ=6，则有3t+2t=6，
解得：t=
；
如图3：
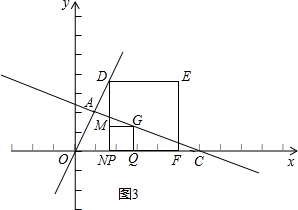
当点P、点N重合时，有OP+CN=6，则有t+2t+
t=6，
解得：t=
，
如图4：
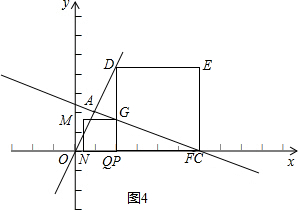
当点P、点Q重合时，有OP+CQ=6，则有t+2t=6，
解得：t=2．
故此刻t的值为：t1=
，t2=
，t3=
，t4=2．
解：（1）∵二次函数y1=ax2+3x+c的图象经过原点及点A（1，2），∴将（0，0），代入得出：
c=0，
将（1，2）代入得出：
a+3=2，
解得：a=-1，
故二次函数解析式为：y1=-x2+3x，
∵图象与x轴相交于另一点B，
∴0=-x2+3x，
解得：x=0或3，
则B（3，0）；
（2）①由已知可得C（6，0）
如图：过A点作AH⊥x轴于H点，
∵DP∥AH，
∴△OPD∽△OHA，
∴
| OP |
| PD |
| OH |
| AH |
即
| a |
| PD |
| 1 |
| 2 |
∴PD=2a，
∵正方形PDEF，
∴E（3a，2a），
∵E（3a，2a）在二次函数y1=-x2+3x的图象上，
∴a=
| 7 |
| 9 |
即OP=
| 7 |
| 9 |
②如图1：
当点F、点N重合时，有OF+CN=6，
∵直线AO过点（1，2），
故直线解析式为：y=2x，
当OP=t，
则AP=2t，
∵直线AC过点（1，2），（6，0），
代入y=ax+b，
|
解得：
|
故直线AC的解析式为：y=-
| 2 |
| 5 |
| 12 |
| 5 |
∵当OP=t，QC=2t，
∴QO=6-2t，
∴GQ=-
| 2 |
| 5 |
| 12 |
| 5 |
| 4 |
| 5 |
即NQ=
| 4 |
| 5 |
∴OP+PN+NQ+QC=6，
则有3t+2t+
| 4 |
| 5 |
解得：t=
| 30 |
| 29 |
如图2：
当点F、点Q重合时，有OF+CQ=6，则有3t+2t=6，
解得：t=
| 6 |
| 5 |
如图3：
当点P、点N重合时，有OP+CN=6，则有t+2t+
| 4 |
| 5 |
解得：t=
| 30 |
| 19 |
如图4：
当点P、点Q重合时，有OP+CQ=6，则有t+2t=6，
解得：t=2．
故此刻t的值为：t1=
| 30 |
| 29 |
| 6 |
| 5 |
| 30 |
| 19 |
点评：此题主要考查了二次函数的综合应用以及相似三角形的判定与性质以及待定系数法求解析式，根据已知结合图象分类讨论得出t的值是解题关键．
练习册系列答案
相关题目
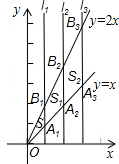（2012•宁波模拟）如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…，直线ln⊥x轴于点（n，0）（n为正整数）．函数y=x的图象与直线l1，l2，l3，…，ln分别交于点A1，A2，A3，…，An；函数y=2x的图象与直线l1，l2，l3，…，ln分别交于点B1，B2，B3，…，Bn．如果△OA1B1的面积记作S，四边形A1A2B2B1的面积记作S1，四边形A2A3B3B2的面积记作S2，…，四边形AnAn+1Bn+1Bn的面积记作Sn，那么S1=