题目内容
（2012•宁波模拟）（1）如图1，正三角形ABC内接于⊙O，P是劣弧BC上的任意一点，连接PB、PC，求证：PB+PC=PA．
（2）如图2，四边形ABCD中，△ABM与△CDN是分别以AB、CD为一边的圆的内接正三角形，E、F分别在这两个三角形的外接圆上．请指出E、F两点的位置，使得AE+EB+EF+FC+FD的值最小，并证明你的结论．
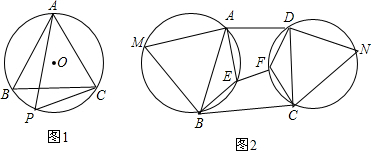
（2）如图2，四边形ABCD中，△ABM与△CDN是分别以AB、CD为一边的圆的内接正三角形，E、F分别在这两个三角形的外接圆上．请指出E、F两点的位置，使得AE+EB+EF+FC+FD的值最小，并证明你的结论．
分析：（1）在PA上截取PD=PB，连结BD，根据等边三角形的性质得∠ABC=∠ACB=60°，AB=CB，再根据圆周角定理得∠BPD=∠ACB=60°，则可判断△PBD为等边三角形，所以
∠PBD=60°，BD=BP，易得∠ABD=∠CBP，然后根据“SAS”可判断△ABD≌△CBP，则AD=CP，于是可得到结论；
（2）连结ME、NF，利用（1）的结论得EA+EB=ME，FC+FD=FN，则AE+EB+EF+FC+FD=ME+EF+FN，然后根据两点之间线段最短得到当点M、E、F、N共线时，ME+EF+FN的值最小．
∠PBD=60°，BD=BP，易得∠ABD=∠CBP，然后根据“SAS”可判断△ABD≌△CBP，则AD=CP，于是可得到结论；
（2）连结ME、NF，利用（1）的结论得EA+EB=ME，FC+FD=FN，则AE+EB+EF+FC+FD=ME+EF+FN，然后根据两点之间线段最短得到当点M、E、F、N共线时，ME+EF+FN的值最小．
解答：（1）证明：在PA上截取PD=PB，连结BD，如图，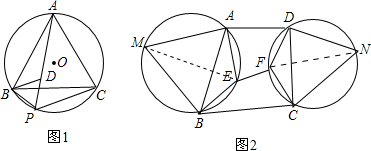
∵△ABC为等边三角形，
∴∠ABC=∠ACB=60°，AB=CB，
∴∠BPD=∠ACB=60°，
∴△PBD为等边三角形，
∴∠PBD=60°，BD=BP，
∴∠ABC-∠DBC=∠PBD-∠DBC，即∠ABD=∠CBP，
∵在△ABD和△CBP中，
，
∴△ABD≌△CBP（SAS），
∴AD=CP，
∴AP=AD+DP=CP+BP，
即PB+PC=PA；
（2）当点E、F为直线MN与两圆的交点时，AE+EB+EF+FC+FD的值最小．
证明：连结ME、NF，如图，
由（1）的结论得EA+EB=ME，FC+FD=FN，
∴AE+EB+EF+FC+FD=ME+EF+FN，
∴当点M、E、F、N共线时，ME+EF+FN的值最小，
此时点E、F为直线MN与两圆的交点．
∵△ABC为等边三角形，
∴∠ABC=∠ACB=60°，AB=CB，
∴∠BPD=∠ACB=60°，
∴△PBD为等边三角形，
∴∠PBD=60°，BD=BP，
∴∠ABC-∠DBC=∠PBD-∠DBC，即∠ABD=∠CBP，
∵在△ABD和△CBP中，
|
∴△ABD≌△CBP（SAS），
∴AD=CP，
∴AP=AD+DP=CP+BP，
即PB+PC=PA；
（2）当点E、F为直线MN与两圆的交点时，AE+EB+EF+FC+FD的值最小．
证明：连结ME、NF，如图，
由（1）的结论得EA+EB=ME，FC+FD=FN，
∴AE+EB+EF+FC+FD=ME+EF+FN，
∴当点M、E、F、N共线时，ME+EF+FN的值最小，
此时点E、F为直线MN与两圆的交点．
点评：本题考查了圆的综合题：圆周角定理是圆中证明角相等常用的定理；熟练掌握等边三角形的判定与性质以及三角形全等的判定与性质；运用两点之间线段最短解决几何中的最小值问题．
练习册系列答案
相关题目
（2012•宁波模拟）如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…，直线ln⊥x轴于点（n，0）（n为正整数）．函数y=x的图象与直线l1，l2，l3，…，ln分别交于点A1，A2，A3，…，An；函数y=2x的图象与直线l1，l2，l3，…，ln分别交于点B1，B2，B3，…，Bn．如果△OA1B1的面积记作S，四边形A1A2B2B1的面积记作S1，四边形A2A3B3B2的面积记作S2，…，四边形AnAn+1Bn+1Bn的面积记作Sn，那么S1=