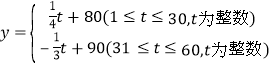Question

【题目】课本“目标与评定”中有这样一道思考题：如图钢架中∠A=20°，焊上等边的钢条P1P2，P2P3，P3P4，P4P5…来加固钢架，若P1A=P1P2，问这样的钢条至多需要多少根？

（1）请将下列解答过程补充完整：

答案：∵∠A=20°，P1A=P1P2，∴∠P1P2A=　 　.

又P1P2=P2P3=P3P4=P4P5，∴∠P2P1P3=P2P3P1=40°，

同理可得，∠P3P2P4=P3P4P2=60°，∠P4P3P5=P4P5P3=　 　，

∴∠BP4P5=∠CP5P4=100°＞90°，

∴对于射线P4B上任意一点P6（点P4除外），P4P5＜P5P6，

∴这样的钢架至多需要　 　根.

（2）继续探究：当∠A=15°时，这样的钢条至多需要多少根？

（3）当这样的钢条至多需要8根时，探究∠A的取值范围.

Answer 1

【答案】（1）∠A；80°；4；（2）这样的钢条至多需要5根；（3）

【解析】

（1）由于焊上的钢条的长度相等，并且P1A=P1P2，所以∠P1P2A=∠A，则可算出∠P2P1P3的度数，并且和∠P1P3P2的度数相等，根据平角的度数为180°和三角形内角和为180°，结合等腰三角形底角度数小于90度即可求出最多能焊上的钢条数；