��Ŀ����
 ��֪���κ���y=-
��֪���κ���y=-| 1 |
| 2 |
| 3 |
| 2 |
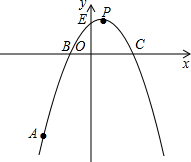
��1����������κ�������ʽ��
��2�����DΪ�߶�OC�ϵ�һ�㣬�������DPC=��BAC��˵��ֱ��PC��ֱ��AC��λ�ù�ϵ���������D�����꣮
��3���ڣ�1���е����������Ƿ����һ��F��ʹS��BCF=
| 3 |
| 4 |
��������1����A�������������y=-
x2+mx+
�����m���Ӷ�ȷ�����κ����Ľ���ʽ��
��2���ȰѶ��κ�����ɶ���ʽ�õ�����P������Ϊ��1��2�������D����Ϊ��a��0��������P��PH��x�ᣬ����ΪH������A��AQ��x�ᣬ����ΪQ�����ݵ������ɵõ�
��PCH�͡�AQC���ǵ���ֱ�������Σ����PCH=45�㣬��ACQ=45�㣬���ǵõ�ֱ��PC��ֱ��AC��ֱ���ɡ�DPC=��BAC����PCD=��ACB�õ���PDC��Rt��ABC���������Ʊ���
=
����
=
�����a=
���Ӷ��õ�D�����ꣻ
��3���ȼ����S��BCP=4����S��BCF=
S��BCP=3����F��������x��y������
��4��|y|=3�����y=
��-
��Ȼ��ֱ������κ�������ʽ�������Ӧ��x��ֵ���Ӷ��õ�F������꣮
| 1 |
| 2 |
| 3 |
| 2 |
��2���ȰѶ��κ�����ɶ���ʽ�õ�����P������Ϊ��1��2�������D����Ϊ��a��0��������P��PH��x�ᣬ����ΪH������A��AQ��x�ᣬ����ΪQ�����ݵ������ɵõ�
��PCH�͡�AQC���ǵ���ֱ�������Σ����PCH=45�㣬��ACQ=45�㣬���ǵõ�ֱ��PC��ֱ��AC��ֱ���ɡ�DPC=��BAC����PCD=��ACB�õ���PDC��Rt��ABC���������Ʊ���
| DC |
| BC |
| PC |
| AC |
| 3-a |
| 4 |
2
| ||
6
|
| 5 |
| 3 |
��3���ȼ����S��BCP=4����S��BCF=
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
����⣺��1��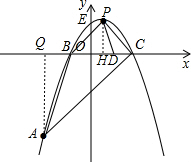 �ߵ�A��-3��-6�����������ϣ�
�ߵ�A��-3��-6�����������ϣ�
��-6=-
��9-3m+
��
���m=1��
��������κ����ı���ʽΪy=-
x2+x+
��
��2����y=-
x2+x+
=-
��x-1��2+2��
��P��������1��2����
��ͼ�����D����Ϊ��a��0��������P��PH��x�ᣬ����ΪH��
����A��AQ��x�ᣬ����ΪQ��
��y=0��-
x2+x+
=0�����x1=-1��x2=3��
��B��������-1��0����C��������3��0��
��P��1��2����A��-3��-6����
��PH=HC=2��QA=QC=6��
���PCH�͡�AQC���ǵ���ֱ�������Σ�
���PCH=45�㣬��ACQ=45�㣬
���PCA=90�㣬
��PC��CA��
�ߡ�DPC=��BAC����PCD=��ACB��
���PDC��Rt��ABC��
��
=
����
=
�����a=
��
��D������
��0����
��3�����ڣ�
��S��BCP=
��4��2=4��
��S��BCF=
S��BCP��
��S��BCF=3��
��F��������x��y��
��
��4��|y|=3��
��y=
��-
��
��y=
ʱ��-
x2+x+
=
�����x1=0��x2=2��
��y=-
ʱ��-
x2+x+
=-
�����x1=1+
��x2=1-
��
��F��0��
����2��
����1+
��-
����1-
��-
����
 �ߵ�A��-3��-6�����������ϣ�
�ߵ�A��-3��-6�����������ϣ���-6=-
| 1 |
| 2 |
| 3 |
| 2 |
���m=1��
��������κ����ı���ʽΪy=-
| 1 |
| 2 |
| 3 |
| 2 |
��2����y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
��P��������1��2����
��ͼ�����D����Ϊ��a��0��������P��PH��x�ᣬ����ΪH��
����A��AQ��x�ᣬ����ΪQ��
��y=0��-
| 1 |
| 2 |
| 3 |
| 2 |
��B��������-1��0����C��������3��0��
��P��1��2����A��-3��-6����
��PH=HC=2��QA=QC=6��
���PCH�͡�AQC���ǵ���ֱ�������Σ�
���PCH=45�㣬��ACQ=45�㣬
���PCA=90�㣬
��PC��CA��
�ߡ�DPC=��BAC����PCD=��ACB��
���PDC��Rt��ABC��
��
| DC |
| BC |
| PC |
| AC |
| 3-a |
| 4 |
2
| ||
6
|
| 5 |
| 3 |
��D������
| 5 |
| 3 |
��3�����ڣ�
��S��BCP=
| 1 |
| 2 |
��S��BCF=
| 3 |
| 4 |
��S��BCF=3��
��F��������x��y��
��
| 1 |
| 2 |
��y=
| 3 |
| 2 |
| 3 |
| 2 |
��y=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
��y=-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 7 |
��F��0��
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 3 |
| 2 |
| 7 |
| 3 |
| 2 |
���������⿼���˶��κ������ۺ��⣺�ȸ��ݼ�������ȷ���������ϵ�����꣬�����ô���ϵ����ȷ�������ߵĽ���ʽ��Ȼ�����ö��κ��������ʽ���й����⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2013•�����ض�ģ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ�
��2013•�����ض�ģ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ� ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���ac��0����a-b+c��0��
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���ac��0����a-b+c��0��