题目内容
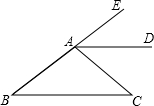 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠C的度数.
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠C的度数.解:∵AD∥BC,
∴∠B=∠
EAD
EAD
.(两直线平行,同位角相等
两直线平行,同位角相等
)又∵∠B=30°,
∴∠
EAD
EAD
=30°.∵AD是∠EAC的平分线,
∴∠DAC=∠
EAD
EAD
,(角平分线的定义
角平分线的定义
)∴∠DAC=
30°
30°
.∵AD∥BC,
∴∠C=∠
DAC
DAC
,(两直线平行,内错角相等
两直线平行,内错角相等
)∴∠C=
30°
30°
.分析:根据平行线的性质,角平分线的定义填空即可.
解答:解:∵AD∥BC,
∴∠B=∠EAD.(两直线平行,同位角相等)
又∵∠B=30°,
∴∠EAD=30°.
∵AD是∠EAC的平分线,
∴∠DAC=∠EAD,(角平分线的定义)
∴∠DAC=30°.
∵AD∥BC,
∴∠C=∠DAC,(两直线平行,内错角相等)
∴∠C=30°.
故答案为:EAD;两直线平行,同位角相等;EAD;EAD;角平分线的定义;30°;DAC;两直线平行,内错角相等;30°.
∴∠B=∠EAD.(两直线平行,同位角相等)
又∵∠B=30°,
∴∠EAD=30°.
∵AD是∠EAC的平分线,
∴∠DAC=∠EAD,(角平分线的定义)
∴∠DAC=30°.
∵AD∥BC,
∴∠C=∠DAC,(两直线平行,内错角相等)
∴∠C=30°.
故答案为:EAD;两直线平行,同位角相等;EAD;EAD;角平分线的定义;30°;DAC;两直线平行,内错角相等;30°.
点评:本题考查了平行线的性质,角平分线的定义,主要在于训练同学们的逻辑思维能力.

练习册系列答案
相关题目
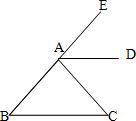 24、如图:AD是∠EAC的平分线,AD∥BC,∠B=45°,你能算出∠EAD、∠DAC、∠C的度数吗?请写出你的解答过程.
24、如图:AD是∠EAC的平分线,AD∥BC,∠B=45°,你能算出∠EAD、∠DAC、∠C的度数吗?请写出你的解答过程.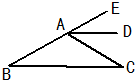
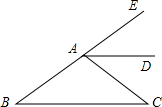 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠EAD、∠DAC、∠C的度数.
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠EAD、∠DAC、∠C的度数.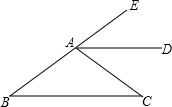 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠C的度数.
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠C的度数.