题目内容
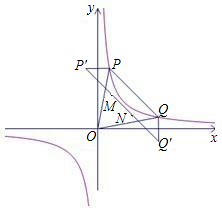
如图,点P(a,b)和点Q(c,d)是反比例函数y=| 1 |
| x |
(1)求证:a=d,b=c;
(2)P1是点P关于y轴的对称点,Q1是点Q关于x轴的对称点,连接P1Q1分别交OP、OQ于点M、N.
①求证:PQ∥P1Q1;
②求四边形PQNM的面积S能否等于
| 8 |
| 5 |
 理由.
理由.
分析:(1)由于点P(a,b)和点Q(c,d)是反比例函数y=
图象上第一象限内的两个点,所以可用含a、c的代数式分别表示b、d,然后由OP=OQ,列出等式,将式子变形,即可得出结果;
(2)①首先求出点P1、Q1的坐标,根据(1)的结论,把点P1、Q1、P、Q四点的坐标都用含a、b的代数式分别表示,然后运用待定系数法分别求出直线PQ与直线P1Q1的解析式,发现它们的斜率相同,因而得出PQ∥P1Q1.
②如果设PP1与y轴交于点A,QQ1与x轴交于点B,过点P作PD⊥x轴于点D,则S△OPQ=S梯形PDBQ=
(a+b)(b-a).设直线MN与y轴交于点E,PQ与y轴交于点C.根据相似三角形的面积比等于相似比的平方,得出S△OMN的值,再根据四边形PQNM的面积S等于
,列出方程,求出解即可.
| 1 |
| x |
(2)①首先求出点P1、Q1的坐标,根据(1)的结论,把点P1、Q1、P、Q四点的坐标都用含a、b的代数式分别表示,然后运用待定系数法分别求出直线PQ与直线P1Q1的解析式,发现它们的斜率相同,因而得出PQ∥P1Q1.
②如果设PP1与y轴交于点A,QQ1与x轴交于点B,过点P作PD⊥x轴于点D,则S△OPQ=S梯形PDBQ=
| 1 |
| 2 |
| 8 |
| 5 |
解答:(1)证明:∵点P(a,b)和点Q(c,d)是反比例函数y=
图象上第一象限内的两个动点(a<b,a≠c),
∴ab=1,cd=1,
即b=
,d=
.
又∵OP=OQ,
∴a2+b2=c2+d2,
即a2+(
)2=(
)2+d2,
∴a4d2+d2=a2+a2d4,
∴a4d2-a2d4=a2-d2,
∴a2d2(a2-d2)-(a2-d2)=0
∴(ad-1)(a-d)=0
∵ad≠1,
∴a=d,
同理可得b=c;
(2)①证明:∵P1是点P(a,b)关于y轴的对称点,∴P1(-a,b),
由(1)知,a=d,b=c,∴Q(c,d)即为Q(b,a),
∵Q1是点Q关于x轴的对称点,∴Q1(b,-a),
运用待定系数法求得直线PQ的解析式为y=-x+a+b,直线P1Q1的解析式为y=-x+b-a,
∴PQ∥P1Q1
②解:如图,设PP1与y轴交于点A,QQ1与x轴交于点B,过点P作PD⊥x轴于点D.
则S△OPQ=S五边形OAPQB-S△OAP-S△OQB=S五边形OAPQB-S△OAP-S△OPD=S梯形PDBQ=
(a+b)(b-a).
设直线MN与y轴交于点E,PQ与y轴交于点C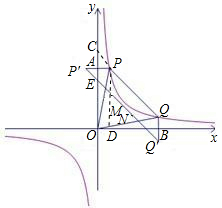 .
.
则C(0,a+b),E(0,b-a)
∵MN∥PQ,∴△OMN∽△OPQ,
∴
=
=
,又OE=b-a,OC=a+b,
∴S△OMN:S△OPQ=(MN:PQ)2=(OE:OC)2=(
)2,
∴S△OMN=
(a+b)(b-a)•(
)2=
•
,
∴S四边形PQNM=S△OPQ-S△OMN=
(a+b)(b-a)-
•
=
(b-a)•
=
(b-a)•
=
,
解得b=9a,
∵ab=1,
∴a=
,b=3.
∴P(
,3).
| 1 |
| x |
∴ab=1,cd=1,
即b=
| 1 |
| a |
| 1 |
| c |
又∵OP=OQ,
∴a2+b2=c2+d2,
即a2+(
| 1 |
| a |
| 1 |
| d |
∴a4d2+d2=a2+a2d4,
∴a4d2-a2d4=a2-d2,
∴a2d2(a2-d2)-(a2-d2)=0
∴(ad-1)(a-d)=0
∵ad≠1,
∴a=d,
同理可得b=c;
(2)①证明:∵P1是点P(a,b)关于y轴的对称点,∴P1(-a,b),
由(1)知,a=d,b=c,∴Q(c,d)即为Q(b,a),
∵Q1是点Q关于x轴的对称点,∴Q1(b,-a),
运用待定系数法求得直线PQ的解析式为y=-x+a+b,直线P1Q1的解析式为y=-x+b-a,
∴PQ∥P1Q1
②解:如图,设PP1与y轴交于点A,QQ1与x轴交于点B,过点P作PD⊥x轴于点D.
则S△OPQ=S五边形OAPQB-S△OAP-S△OQB=S五边形OAPQB-S△OAP-S△OPD=S梯形PDBQ=
| 1 |
| 2 |
设直线MN与y轴交于点E,PQ与y轴交于点C
 .
.则C(0,a+b),E(0,b-a)
∵MN∥PQ,∴△OMN∽△OPQ,
∴
| OM |
| OP |
| OE |
| OC |
| MN |
| PQ |
∴S△OMN:S△OPQ=(MN:PQ)2=(OE:OC)2=(
| b-a |
| a+b |
∴S△OMN=
| 1 |
| 2 |
| b-a |
| a+b |
| 1 |
| 2 |
| (b-a)3 |
| a+b |
∴S四边形PQNM=S△OPQ-S△OMN=
| 1 |
| 2 |
| 1 |
| 2 |
| (b-a)3 |
| a+b |
=
| 1 |
| 2 |
| (a+b)2-(a-b)2 |
| a+b |
| 1 |
| 2 |
| 4 |
| a+b |
| 8 |
| 5 |
解得b=9a,
∵ab=1,
∴a=
| 1 |
| 3 |
∴P(
| 1 |
| 3 |
点评:本题综合考查了运用待定系数法求函数的解析式,反比例函数、相似三角形的性质等知识,难度很大.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是