题目内容
【题目】如图,⊙O的半径为3,A,P两点在⊙O上,点B在⊙O内,tan∠APB=![]() ,AB⊥AP.如果OB⊥OP,那么OB的长为_____.
,AB⊥AP.如果OB⊥OP,那么OB的长为_____.
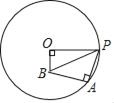
【答案】1
【解析】
如图,连接OA,作AM⊥OB交OB的延长线于M,作PN⊥MA交MA的延长线于N.则四边形POMN是矩形.想办法求出OM、BM即可解决问题;
解:如图,连接OA,作AM⊥OB交OB的延长线于M,作PN⊥MA交MA的延长线于N.则四边形POMN是矩形.
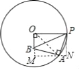
∵∠POB=∠PAB=90°,
∴P、O、B、A四点共圆,
∴∠AOB=∠APB,
∴tan∠AOM=tan∠APB=![]() =
=![]() ,设AM=4k,OM=3k,
,设AM=4k,OM=3k,
在Rt△OMA中,(4k)2+(3k)2=32,
解得k=![]() (负根已经舍弃),
(负根已经舍弃),
∴AM=![]() ,OM=
,OM=![]() ,AN=MN﹣AM=
,AN=MN﹣AM=![]() ,
,
∵∠MAB+∠ABM=90°,∠MAB+∠PAN=90°,
∴∠ABM=∠PAN,∵∠AMB=∠PNA=90°,
∴△AMB∽△PNA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BM=![]() ,
,
∴OB=OM﹣BM=1.
故答案为1

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .