题目内容
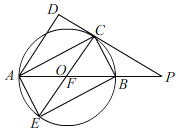
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于点P.
(1)求证:AC2=ADAB.
(2)点E是∠ACB所对的弧上的一个动点(不包括A,B两点),连接EC交直径AB于点F,∠DAP=64°.
①当∠ECB= °时,△PCF为等腰三角形;
②当∠ECB= °时,四边形ACBE为矩形.

【答案】(1)见解析;(2)①45;②58.
【解析】
(1)先判断出∠ACD=∠ABC,再利用直径所对的圆周角等于90度和垂直的定义判断出∠ADC=∠ACB,进而判断出△ADC∽△ACB,即可得出结论;
(2)①先求出∠CAD=32°,判断出∠CAP>∠P,进而判断出CF≠CP,再求出∠BCP=32°>∠P,得出BP>BC,进而判断出CF≠PF,最后用等腰三角形的性质即可得出结论;
②先判断出CE过点O,进而求出∠ACE,即可得出结论.
解:(1)∵CD是⊙O的切线,
∴∠ACD=∠ABC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AD⊥CD,
∴∠ADC=90°=∠ACB,
∴△ADC∽△ACB,
∴![]() ,
,
∴AC2=ABAD;
(2)①由(1)知,∠ACD=∠ABC,
∵∠ACD+∠CAD=90°,∠ABC+∠BAC=90°,
∴∠CAD=∠BAC=![]() ∠DAP=32°,
∠DAP=32°,
∵∠P=90°﹣∠DAP=26°,
∴∠CAP>∠P,
∴CP>AC,
∵点F在直径AB上(且不和点A,B重合),
∴CF≠CP,
∵∠CAD=32°,
∴∠ACD=90°﹣∠CAD=58°,
∵∠ACB=90°,
∴∠BCP=180°﹣∠ACD﹣∠ACB=32°>∠P
∴BP>BC,
∵点F在直径AB上(且不和点A,B重合),
∴CF≠PF,
∵△PCF是等腰三角形,
∴PC=PF,
∴∠PCF=![]() (180°﹣∠P)=77°,
(180°﹣∠P)=77°,
∴∠BCE=∠PCF﹣∠BCP=45°,
故答案为:45;
②如图,
∵四边形ACBE是矩形,
∴AB与CE互相平分,
∵点O是AB的中点,
∴点F和点O重合,
∴∠ACE=∠CAB=32°,
∴∠BCE=90°﹣∠ACE=58°,
故答案为:58.

 名校课堂系列答案
名校课堂系列答案【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )
姓名 | 小红 | 小明 | 小东 | 小亮 | 小丽 | 小华 |
成绩(分) | 110 | 106 | 109 | 111 | 108 | 110 |
A.众数是110B.方差是16
C.平均数是109.5D.中位数是109