题目内容
【题目】在平行四边形ABCD中，AE平分∠BAD交边于点E，DF平分∠ADC交边于点F，若AD
12，EF5，则AB___________．
【答案】
或
【解析】
根据平行四边形的性质以及角平分线的定义可得到AB=BE，DC=CF，对于AE和DF的位置进行分类讨论，①当AE和DF交叉时，②当AE和DF交叉时，分别计算即可．
解：∵四边形ABCD是平行四边形，AD=12，
∴AD∥BC，BC=AD=12，AB=CD
∴∠DAE=∠AEB，
∵AE平分∠BAD，
∴∠DAE=∠BAE，
∴∠AEB=∠BAE
∴AB=BE，
同理，DC=CF
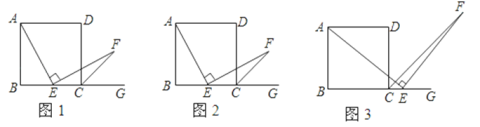
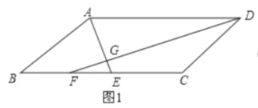
①如图1，当AE和DF交叉时，BE+ CF
BC+ EF
即2AB=12+5=17
所以，AB
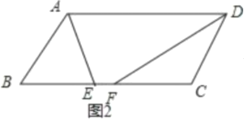
②如图2，当AE和DF不交叉时，BE+ CFBC- EF
即2AB=12-5=7
所以，AB
综上所述，AB或
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】[问题情境]
已知矩形的面积为一定值1，当该矩形的一组邻边分别为多少时，它的周长最小？最小值是多少？
[数学模型]
设该矩形的一边长为x，周长为L，则L与x的函数表达式为 ．
[探索研究]
小彬借鉴以前研究函数的经验，先探索函数
的图象性质．
（1）结合问题情境，函数的自变量x的取值范围是 ，
如表是y与x的几组对应值．
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值；
②画出该函数图象，结合图象，得出当x= 时，y有最小值，y的最小值为 ．
[解决问题]
（2）直接写出“问题情境”中问题的结论．
