题目内容
【题目】如图,△ABC中,∠BAC=90°,沿AD折叠△ABD,使点B恰好落在AC边上的点E处.若∠C=24°,则∠ADE等于( ) 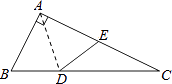
A.66°
B.69°
C.70°
D.71°
【答案】B
【解析】解:在△ABC中,∠CAB=90°,∠C=24°, ∴∠B=90°﹣∠C=66°.
由折叠的性质可得:∠EAD= ![]() ∠CAB=45°,
∠CAB=45°,
∴∠ADE=180°﹣∠EAD﹣∠B
=69°.
故选:B
【考点精析】掌握三角形的内角和外角和翻折变换(折叠问题)是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目