Question

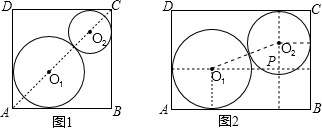
（Ⅰ）如图1，在正方形ABCD内，已知两个动圆⊙O₁与⊙O₂互相外切，且⊙O₁与边AB、AD相切，⊙O₂与边BC、CD相切．若正方形ABCD的边长为1，⊙O₁与⊙O₂的半径分别为r₁，r₂．
①求r₁与r₂的关系式；
②求⊙O₁与⊙O₂面积之和的最小值．
（Ⅱ）如图2，若将（Ⅰ）中的正方形ABCD改为一个宽为1，长为

3

2

的矩形，其他条件不变，则⊙O₁与⊙O₂面积的和是否存在最小值，若不存在，请说明理由；若存在，请求出这个最小值．

Answer 1

分析：（Ⅰ）①连接AC，根据正方形的性质可知，AC平分∠BAD、∠BCD，而AB、AD为⊙O₁的切线，BC、CD为⊙O₂的切线，故O₁与O₂在AC上，解等腰直角三角形得AO1=

2

r1，CO2=

2

r2，AC=

2

，由两圆外切得O₁O₂=r₁+r₂，由AO₁+O₁O₂+O₂C=AC，列方程求关系式；
②由面积之和S=π（r₁²+r₂²）及r1+r2=2-

2

，换元为关于r₁的二次函数，根据r₁的取值范围求S的最小值；
（Ⅱ）如图2，作辅助线，得到Rt△O₁O₂P，用r₁、r₂分别表示△O₁O₂P的三边，用勾股定理可求r₁+r₂的值，根据不等式r12+r22≥

(r1+r2)2

2

求面积和的最小值．

解答：解：（Ⅰ）①如图1，在正方形ABCD中，连接AC，显然O₁与O₂在AC上，
且AO1=

2

r1，O₁O₂=r₁+r₂，CO2=

2

r2，
由AC=AO1+O1O2+CO2=

2

，
∴

2

r1+r1+r2+

2

r2=

2

．
∴r1+r2=2-

2

．
②根据题意，r₁≤

1

2

，r₂≤

1

2

，
可得r2=2-

2

-r1≤

1

2

，即

3

2

-

2

≤r₁≤

1

2

．
∵⊙O₁与⊙O₂的面积之和S=π（r₁²+r₂²），
∴

S

π

=r12+(2-

2

-r1)2
=2r12-2(2-

2

)r1+6-4

2

=2(r1-

2- 2

2

)2+3-2

2

，
这里

3

2

-

2

≤

2- 2

2

≤

1

2

，
∴当r1=

2- 2

2

时，⊙O₁与⊙O₂是等圆，其面积和的最小值为(3-2

2

)π；

（Ⅱ）如图2，作辅助线，得到Rt△O₁O₂P，
则O₁O₂=r₁+r₂，O1P=AB-r1-r2=

3

2

-r1-r2，O₂P=BC-r₁-r₂=1-r₁-r₂．
∵在Rt△O₁O₂P中，O₁O₂²=O₁P²+O₂P²，
∴(r1+r2)2=(

3

2

-r1-r2)2+(1-r1-r2)2．
即(r1+r2)2-5(r1+r2)+

13

4

=0．
解得r1+r2=

5

2

+

3

或r1+r2=

5

2

-

3

．
由于r1+r2＜1+

3

2

=

5

2

，故r1+r2=

5

2

+

3

不合题意，应舍去．
∴r1+r2=

5

2

-

3

．
∵⊙O₁与⊙O₂的面积之和S=π（r₁²+r₂²），
而r12+r22≥

(r1+r2)2

2

，当且仅当r₁=r₂时，等号成立，
∴当r₁=r₂时，⊙O₁与⊙O₂面积和存在最小值，最小值为

( 5 2 - 3 )2

2

π，即(

37

8

-

5

2

3

)π．

点评：本题考查了圆的面积计算，切线、圆与圆相切的性质．关键是根据勾股定理将两圆半径与已知矩形边长联系起来．