题目内容
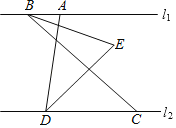
【题目】如图,已知直线l1∥l2,点A、B在直线l1上,点C、D在直线l2上,点C在点D的右侧,∠ADC=80°,∠ABC=n°,BE平分∠ABC,DE平分∠ADC,直线BE、DE交于点E.
(1)写出∠EDC的度数_____;
(2)试求∠BED的度数(用含n的代数式表示);
(3)将线段BC向右平行移动,其他条件不变,请直接写出∠BED的度数(用含n的代数式表示)
【答案】(1)40°;(2)∠BED=![]() n°+40°;(3)∠BED的度数变化,度数为
n°+40°;(3)∠BED的度数变化,度数为![]() n°+40°或220°﹣
n°+40°或220°﹣![]() n°或
n°或![]() n°﹣40°.
n°﹣40°.
【解析】
(1)根据角平分线的定义,即可得到![]() ;
;
(2)过点![]() 作
作![]() ,根据两直线平行,内错角相等可得
,根据两直线平行,内错角相等可得![]() ,
,![]() ,根据角平分线的定义求出
,根据角平分线的定义求出![]() ,
,![]() ,然后求解即可;
,然后求解即可;
(3)过点![]() 作
作![]() ,然后分类讨论:①点
,然后分类讨论:①点![]() 在点
在点![]() 的左边,根据角平分线的定义求出
的左边,根据角平分线的定义求出![]() ,
,![]() ,根据两直线平行,内错角相等可得
,根据两直线平行,内错角相等可得![]() ,
,![]() ,然后求解;②点
,然后求解;②点![]() 在点
在点![]() 的右边时,根据角平分线的定义求出
的右边时,根据角平分线的定义求出![]() ,
,![]() ,根据两直线平行,内错角相等可得
,根据两直线平行,内错角相等可得![]() ,根据两直线平行,同旁内角互补求出
,根据两直线平行,同旁内角互补求出![]() ,然后求解即可.
,然后求解即可.
解:(1)∵![]() 平分
平分![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(2)如图1:

过点![]() 作
作![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(3)过点![]() 作
作![]() ,
,
①如图1:

点![]() 在点
在点![]() 的右边时,
的右边时,
过点![]() 作
作![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
②如图2:
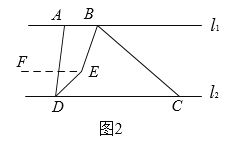
点![]() 在点
在点![]() 的左边时,若点
的左边时,若点![]() 在直线
在直线![]() 和
和![]() 之间,则
之间,则
过点![]() 作
作![]() ,
,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
③如图3:
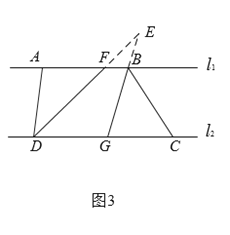
点![]() 在点
在点![]() 的左边时,若点
的左边时,若点![]() 在直线
在直线![]() 的上方,则,
的上方,则,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
④如图4:
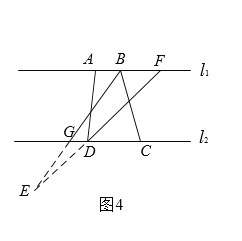
点![]() 在点
在点![]() 的左边时,若点
的左边时,若点![]() 在直线
在直线![]() 的下方,则
的下方,则
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴将线段BC向右平行移动,其他条件不变,∠BED的度数为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目