题目内容
【题目】如图,边长为4的正方形ABCD内接于点O,点E是 ![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是 ![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论: ①
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论: ① ![]() =
= ![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+ ![]() .
.
其中正确的是(把你认为正确结论的序号都填上).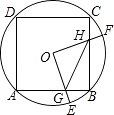
【答案】①②
【解析】解:①如图所示,
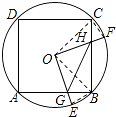
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,
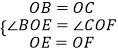 ,
,
∴△BOE≌△COF,
∴BE=CF,
∴ ![]() =
= ![]() ,①正确;②∵BE=CF,
,①正确;②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.③如图所示,
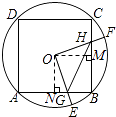
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4﹣x,
则GH= ![]() =
= ![]() ,
,
∴其最小值为4+2 ![]() ,D错误.
,D错误.
所以答案是:①②.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
【题目】某公司有2位股东,20名工人、从2006年至2008年,公司每年股东的总利润和每年工人的工资总额如图所示.
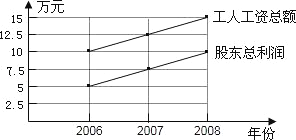
(1)填写下表:
年份 | 2006年 | 2007年 | 2008年 |
工人的平均工资/元 | 5000 | ||
股东的平均利润/元 | 25000 |
(2)假设在以后的若干年中,每年工人的工资和股东的利润都按上图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的8倍?




