Question

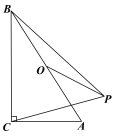
【题目】如图，△ABC中，∠C=90°，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B的路径运动，且速度为每秒1cm，设出发的时间为t秒．问t为何值时，△BCP为等腰三角形？

Answer 1

【答案】3s、5.4s、6s、6.5s

【解析】

试题因为AB与CB，由勾股定理得AC=4 因为AB为5cm，所以必须使AC=CB，或CB=AB，所以必须使AC或AB等于3，有两种情况，△BCP为等腰三角形．

试题解析：由∠C=90°，AB=5cm，BC=3cm，

∴AC=4，

①若P在边AC上时，BC=CP=3cm，

此时用的时间为3s，△BCP为等腰三角形；

②若P在AB边上时，有三种情况：

i）若使BP=CB=3cm，此时AP=2cm，P运动的路程为2+4=6cm，

所以用的时间为6s，△BCP为等腰三角形；

ii）若CP=BC=3cm，过C作斜边AB的高，根据面积法求得高为2.4cm，

作CD⊥AB于点D，

在Rt△PCD中，PD=1.8，

所以BP=2PD=3.6cm，

所以P运动的路程为9-3.6=5.4cm，

则用的时间为5.4s，△BCP为等腰三角形；

ⅲ）若BP=CP，此时P应该为斜边AB的中点，P运动的路程为4+2.5=6.5cm

则所用的时间为6.5s，△BCP为等腰三角形；

综上所述，当t为3s、5.4s、6s、6.5s时，△BCP为等腰三角形．