题目内容
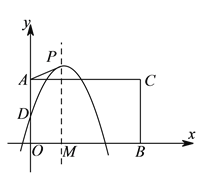
【题目】如图,在平面直角坐标系中,点![]() ,
, ![]() 分别是
分别是![]() 轴正半轴,
轴正半轴, ![]() 轴正半轴上两动点,
轴正半轴上两动点, ![]() ,
, ![]() ,以
,以![]() ,
, ![]() 为邻边构造矩形
为邻边构造矩形![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
, ![]() 为顶点,
为顶点, ![]() 轴于点
轴于点![]() .
.
(![]() )求
)求![]() ,
, ![]() 的长(结果均用含
的长(结果均用含![]() 的代数式表示);
的代数式表示);
(![]() )当
)当![]() 时,求该抛物线的表达式;
时,求该抛物线的表达式;
(![]() )在点
)在点![]() 在整个运动过程中,若存在
在整个运动过程中,若存在![]() 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的![]() 的值.
的值.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)点D在y=-![]() x2+3x+k上,且在y轴上,即y=0求出点D坐标,根据抛物线顶点公式,求出即可;
x2+3x+k上,且在y轴上,即y=0求出点D坐标,根据抛物线顶点公式,求出即可;
(2)先用k表示出相关的点的坐标,根据PM=BM建立方程即可;
(3)先用k表示出相关的点的坐标,根据△ADP是等腰三角形,分三种情况,AD=AP,DA=DP,PA=PD计算.
试题解析:( ![]() )把
)把![]() 代入
代入![]() ,
, ![]() ,
,
∴![]() ,
,
∵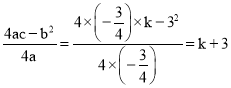 ,
,
∴![]() .
.
(![]() )∵
)∵ ,
,
∴![]() ,
, ![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
抛物线表达式为![]() .
.
(![]() )当
)当![]() 在矩形
在矩形![]() 外时,
外时,
如图![]() ,过
,过![]() 作
作![]() 于
于![]() 点,
点,
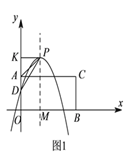
当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
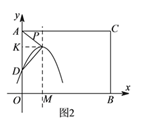
当![]() 在矩形
在矩形![]() 内部时,
内部时,
![]() 时,如图
时,如图![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
又∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
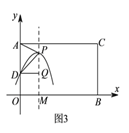
当![]() 时,如图3,过
时,如图3,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() .
.

练习册系列答案
相关题目