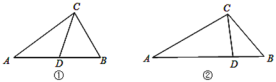题目内容
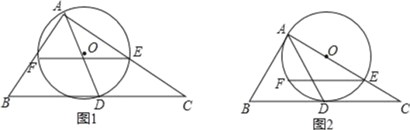
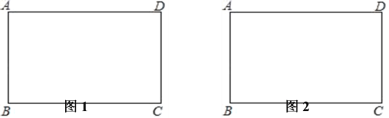
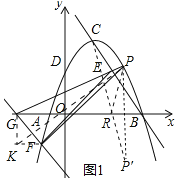
【题目】如图1,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点D,点C为抛物线的顶点,过B,C两点作直线BC,抛物线上的一点F的横坐标是
与x轴交于A,B两点(点A在点B左侧),与y轴交于点D,点C为抛物线的顶点,过B,C两点作直线BC,抛物线上的一点F的横坐标是![]() ,过点F作直线FG//BC交x轴于点G.
,过点F作直线FG//BC交x轴于点G.
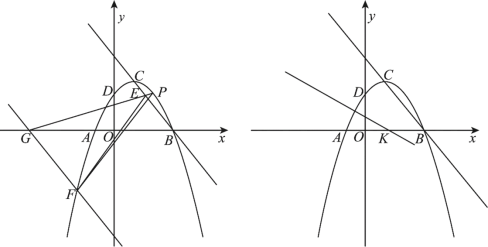
(1)点P是直线BC上方抛物线上的一动点,连接PG与直线BC交于点E,连接EF,PF,当![]() 的面积最大时,在x轴上有一点R,使PR+CR的值最小,求出点R的坐标,并直接写出PR+CR的最小值;
的面积最大时,在x轴上有一点R,使PR+CR的值最小,求出点R的坐标,并直接写出PR+CR的最小值;
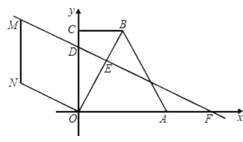
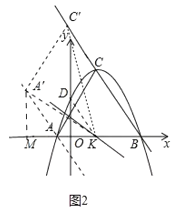
(2)如图2,连接AD,作AD的垂直平分线与x轴交于点K,平移抛物线,使抛物线的顶点C在射线BC上移动,平移的距离是t,平移后抛物线上点A,点C的对应点分别为点A′,点C′,连接A′C′,A′K,C′K,![]() A′C′K是否能为等腰三角形?若能,求出t的值;若不能,请说明理由.
A′C′K是否能为等腰三角形?若能,求出t的值;若不能,请说明理由.
【答案】(1)点R坐标为(![]() ,0),
,0),![]() ;(2)存在,t的值为
;(2)存在,t的值为![]() 或
或![]() .
.
【解析】
(1)首先求出B、C两点坐标,即可确定直线BC的解析式,求出FG的解析式即可求出点G的坐标,如图1中,过点G作y轴的平行线,过F作x轴的平行线交于点K,连接PK.设P(m,![]() ),因为BC∥FG,FG是定值,所以△EFG的面积是定值,所以△PFG的面积最大时,△PEF的面积最大,构建二次函数,利用二次函数的性质求出点P坐标,作P关于x轴的对称点P′,连接P′C交x轴于R,此时CR+RP最小,由此即可解决问题.
),因为BC∥FG,FG是定值,所以△EFG的面积是定值,所以△PFG的面积最大时,△PEF的面积最大,构建二次函数,利用二次函数的性质求出点P坐标,作P关于x轴的对称点P′,连接P′C交x轴于R,此时CR+RP最小,由此即可解决问题.
(2)分三种情形讨论即可:①当KA′=A′C′时,②当C′A′=C′K时,③当KA′=KC′时,分别列出方程求解即可.
解:(1)对于抛物线![]() ,另y=0得到
,另y=0得到![]() ,
,
解得:![]() 或
或![]() ,
,
∴点B坐标为(![]() ,0),
,0),
∵![]() ,
,
∴顶点C的坐标为:(![]() ,4),
,4),
设直线BC解析式为y=kx+b,
则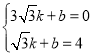 ,解得:
,解得: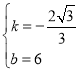 ,
,
∴直线BC解析式为:![]() ,
,
将F的横坐标代入抛物线解析式可得:F(![]() ,-5),
,-5),
∵FG//BC,
∴直线FG解析式为:![]() ,
,
令y=0得到![]() ,
,
∴点G坐标为:(![]() ),
),
如图1中,过点G作y轴的平行线,过F作x轴的平行线交于点K,连接PK.
设P(m,![]() ),
),
∵BC∥FG,FG是定值,
∴△EFG的面积是定值,
∴△PFG的面积最大时,△PEF的面积最大,
∵S△PFG=S△PGK+S△PFK-S△FGK=![]()
![]() ,
,
∵![]() <0,
<0,
∴m=![]() 时,△PFG的面积最大,即△PEF的面积最大,
时,△PFG的面积最大,即△PEF的面积最大,
∴P(![]() ,3),
,3),
作P关于x轴的对称点P′(![]() ,-3),连接P′C交x轴于R,此时CR+RP最小,
,-3),连接P′C交x轴于R,此时CR+RP最小,
最小值=CP′=![]() ,
,
设直线P′C的解析式为:![]() ,
,
则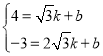 ,解得:
,解得: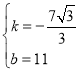
∴直线P′C的解析式为![]() ,
,
当y=0时,![]() ,
,
∴点R坐标为(![]() ,0);
,0);
(2)如图2中,连接DK,DA,
∵A(![]() ),D(0,3),
),D(0,3),
∴OA=![]() ,DO=3,
,DO=3,
∴tan∠DAO=![]() ,
,
∴∠DAO=60°,
∵KA=KD,
∴△ADK是等边三角形,
∴AD=AK=![]() ,K(
,K(![]() ,
,
①∵A(![]() ,0),C(
,0),C(![]() ,4),
,4),
∴AC=![]() ,
,
当KA′=A′C′=AC=![]() 时,
时,
∵AA′=t,tan∠A′AM=tan∠ABC=![]() ,
,
∴sin∠A′AM=sin∠ABC=![]() ,
,
∴A′M=![]() ,AM=
,AM=![]() ,
,
在Rt△A′MK中,A′K2=A′M2+KM2=![]() +(
+(![]() )2,
)2,
∴![]() +(
+(![]() )2=(
)2=(![]() )2,
)2,
解得:![]() 或
或![]() (舍去);
(舍去);
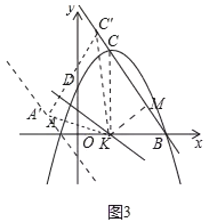
②如图3,当C′A′= C′K时,连接CK,作KM⊥BC于M,
在Rt△BCK中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴C′K2=KM2+ C′M2=![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
③当KA′= KC′时,![]() +(
+(![]() )2=
)2=![]() ,
,
解得:![]() (舍去),
(舍去),
综上所述,当△A′C′K为等腰三角形时,t的值为![]() 或
或![]() .
.

 小学课时特训系列答案
小学课时特训系列答案