题目内容
【题目】如图,已知直线![]() 分别交x轴、y轴于A、B两点,抛物线
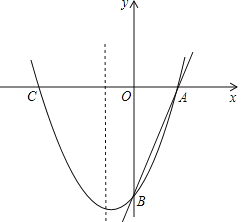
分别交x轴、y轴于A、B两点,抛物线![]() 经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
【答案】(1)![]() ;(2)6;(3)M1(﹣1,
;(2)6;(3)M1(﹣1,![]() ),M2(﹣1,
),M2(﹣1,![]() ),M3(﹣1,0),M4(﹣1,﹣1)
),M3(﹣1,0),M4(﹣1,﹣1)
【解析】试题分析:(1)由直线解析式求出点A及点B的坐标,将点A及点B的坐标代入抛物线解析式,可得出b、c的值,即可求出抛物线解析式;
(2)由(1)求得的抛物线解析式,求出点C的坐标,从而求出AC的长度,代入三角形的面积公式即可计算;
(3)根据点M在抛物线对称轴上,可设点M的坐标为(﹣1,m),分三种情况讨论,①MA=BA,②MB=BA,③MB=MA,列方程,求出m的值后即可.
试题解析:(1)∵直线![]() 分别交x轴、y轴于A、B两点,∴可得A(1,0),B(0,﹣3),把A、B两点的坐标分别代入
分别交x轴、y轴于A、B两点,∴可得A(1,0),B(0,﹣3),把A、B两点的坐标分别代入![]() 得:
得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为:
,∴抛物线解析式为:![]() ;
;
(2)令y=0得:![]() ,解得:
,解得:![]() ,
,![]() ,则C点坐标为:(﹣3,0),AC=4,故可得S△ABC=
,则C点坐标为:(﹣3,0),AC=4,故可得S△ABC=![]() AC×OB=
AC×OB=![]() ×4×3=6;
×4×3=6;
(3)存在,理由如下:抛物线的对称轴为:x=﹣1,假设存在M(﹣1,m)满足题意:分三种情况讨论:
①当MA=AB时,∵OA=1,OB=3,∴AB=![]() ,
,![]() ,解得:m=
,解得:m=![]() ,∴M1(﹣1,
,∴M1(﹣1,![]() ),M2(﹣1,
),M2(﹣1,![]() );
);
②当MB=BA时,![]() ,解得:M3=0,M4=﹣6,∴M3(﹣1,0),M4(﹣1,﹣6)(不合题意舍去);
,解得:M3=0,M4=﹣6,∴M3(﹣1,0),M4(﹣1,﹣6)(不合题意舍去);
③当MB=MA时,![]() ,解得:m=﹣1,∴M5(﹣1,﹣1),答:共存在4个点M1(﹣1,
,解得:m=﹣1,∴M5(﹣1,﹣1),答:共存在4个点M1(﹣1,![]() ),M2(﹣1,
),M2(﹣1,![]() ),M3(﹣1,0),M4(﹣1,﹣1)使△ABM为等腰三角形.
),M3(﹣1,0),M4(﹣1,﹣1)使△ABM为等腰三角形.




