题目内容
若抛物线y=ax2+x+2经过点(-1,0).(1)求a的值,并写出这个抛物线的顶点坐标;
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
分析:(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
解答:解:(1)∵抛物线经过点(-1,0),
∴(-1)2•a+(-1)+2=0,解得a=-1.
∴抛物线y=-x2+x+2的顶点坐标为(
,
).
(2)根据题意,得-t2+t+2=t.解得t=±
,
∴这个抛物线上有两个不动点,坐标分别为(
,
)和(-
,-
).
∴(-1)2•a+(-1)+2=0,解得a=-1.
∴抛物线y=-x2+x+2的顶点坐标为(
| 1 |
| 2 |
| 9 |
| 4 |
(2)根据题意,得-t2+t+2=t.解得t=±
| 2 |
∴这个抛物线上有两个不动点,坐标分别为(
| 2 |
| 2 |
| 2 |
| 2 |
点评:此题考查了抛物线解析式的确定以及函数图象上点的坐标意义,属基础题,需要熟练掌握.

练习册系列答案
相关题目
 .问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (2013•镇江模拟)已知抛物线y=ax2+bx经过点A(-3,-3)和点P(t,0),且t≠0.
(2013•镇江模拟)已知抛物线y=ax2+bx经过点A(-3,-3)和点P(t,0),且t≠0. (2013•平谷区一模)如图,在直角坐标系中,已知直线
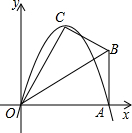
(2013•平谷区一模)如图,在直角坐标系中,已知直线