��Ŀ����
 ��2013•ƽ����һģ����ͼ����ֱ������ϵ�У���ֱ֪��y=
��2013•ƽ����һģ����ͼ����ֱ������ϵ�У���ֱ֪��y=| 1 |
| 2 |
��1����C������Ϊ
��-3��2��
��-3��2��
����D��������-1��3��
��-1��3��
����2����������y=ax2+bx+2��a��0������C��D���㣬��������ߵĽ���ʽ��
��3������������ÿ��
| 5 |
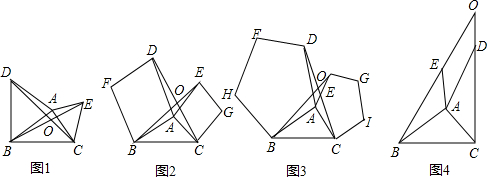
��������1������ȫ�������Σ���ȫ�������ζ�Ӧ�߶�֮�����ȹ�ϵ�������C����D�����ꣻ
��2����C��D������������y=ax2+bx+2�����ô���ϵ������������ߵĽ���ʽ��
��3��Ϊ��s�ı���ʽ����Ҫʶ�������Σ��������ߣ����˶����̣������ε�ƽ�ƣ��ӿ�ʼ���������ܹ���ʱ
�룬�ڼ���Ի��ֳ������Σ���0��t��
ʱ����Ӧͼ2����
��t��1ʱ����Ӧͼ3����1��t��
ʱ����Ӧͼ4��ÿ���εı���ʽ��ͬ�������ͼ������˼����
��2����C��D������������y=ax2+bx+2�����ô���ϵ������������ߵĽ���ʽ��
��3��Ϊ��s�ı���ʽ����Ҫʶ�������Σ��������ߣ����˶����̣������ε�ƽ�ƣ��ӿ�ʼ���������ܹ���ʱ
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
���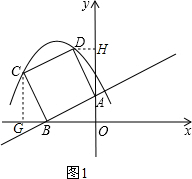 �⣺��1����y=
�⣺��1����y=
x+1��
�൱x=0ʱ��y=1����A������Ϊ��0��1����
��y=0ʱ��x=-2����B������Ϊ��-2��0����
��ͼ1����D����DH��y����H����C����CG��x����G��
��֤��ADH�ա�BAO����DH=OA=1��AH=OB=2����D��-1��3����
ͬ����CBG�ա�BAO����BG=OA=1��CG=OB=2����C��-3��2����
�ʴ�Ϊ��-3��2������-1��3����
��2����C��-3��2����D��-1��3��������������y=ax2+bx+2��
��
�����
��
��y=-
x2-
x+2��
 ��3���ٵ���D�˶���y����ʱ��t=
��3���ٵ���D�˶���y����ʱ��t=
��
��0��t��
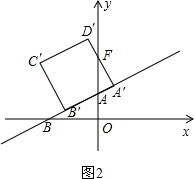
ʱ����ͼ2����D��A�佻y���ڵ�F��
��tan��BAO=
=2���֡ߡ�BAO=��FAA�䣬
��tan��FAA��=2����
=2��
��AA��=
t����FA��=2
t��?
��S��AA��F?=
AA��•FA��=
��
t��2
t=5t2��?
����B�˶�����Cʱ��t=1��
�� ��
��
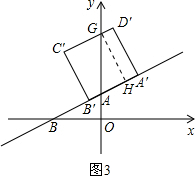
��t��1ʱ����ͼ3����D��C�佻y���ڵ�G����G��GH��B��A����H��
��Rt��BOA��BA=
=
��
��GH=
����AH=
GH=
��
��AA��=
t����HA��=
t-
����GD��=
t-
��
��S����AA��D��G?=
��
t-
+
t��
=5t-
��
����E�˶���y����ʱ��t=
��
�۵�1��t��
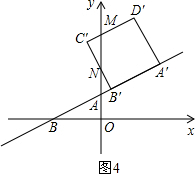
ʱ����ͼ4����D��E�䡢E��B��ֱ�y���ڵ�M��N��
��AA��=
t��B��A��=
��
��AB��=
t-
��?��B��N=2AB��=2
t-2
��
 ��B��C��=
��B��C��=
����C��N=B��C��-B��N=3
-2
t��
��C��M=
C��N=
��3
-2
t����
��S��MNC��=
��3
-2
t��•
��3
-2
t��=5t2-15t+
��
��S�����B��A��D��MN?=S������B��A��D��C��?-S��MNC��=��
��2-��5t2-15t+
��=-5t2+15t-
��
����������S��x�ĺ�����ϵʽΪ��
��0��t��
ʱ��S=5t2��
��
��t��1ʱ��S=5t-
��
��1��t��
ʱ��S=-5t2+15t-
��
 �⣺��1����y=
�⣺��1����y=| 1 |
| 2 |
�൱x=0ʱ��y=1����A������Ϊ��0��1����
��y=0ʱ��x=-2����B������Ϊ��-2��0����
��ͼ1����D����DH��y����H����C����CG��x����G��
��֤��ADH�ա�BAO����DH=OA=1��AH=OB=2����D��-1��3����
ͬ����CBG�ա�BAO����BG=OA=1��CG=OB=2����C��-3��2����
�ʴ�Ϊ��-3��2������-1��3����
��2����C��-3��2����D��-1��3��������������y=ax2+bx+2��
��
|
|
��y=-
| 1 |
| 2 |
| 3 |
| 2 |
 ��3���ٵ���D�˶���y����ʱ��t=
��3���ٵ���D�˶���y����ʱ��t=| 1 |
| 2 |
��0��t��
| 1 |
| 2 |
��tan��BAO=
| OB |
| OA |
��tan��FAA��=2����
| FA�� |
| AA�� |
��AA��=
| 5 |
| 5 |
��S��AA��F?=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
����B�˶�����Cʱ��t=1��
��
 ��
��| 1 |
| 2 |
��Rt��BOA��BA=
| 22+12 |
| 5 |
��GH=
| 5 |
| 1 |
| 2 |
| ||
| 2 |
��AA��=
| 5 |
| 5 |
| ||
| 2 |
| 5 |
| ||
| 2 |
��S����AA��D��G?=
| 1 |
| 2 |
| 5 |
| ||
| 2 |
| 5 |
| 5 |
| 5 |
| 4 |
����E�˶���y����ʱ��t=
| 3 |
| 2 |
�۵�1��t��
| 3 |
| 2 |
��AA��=
| 5 |
| 5 |
��AB��=
| 5 |
| 5 |
| 5 |
| 5 |
 ��B��C��=
��B��C��=| 5 |
| 5 |
| 5 |
��C��M=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
��S��MNC��=
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
| 45 |
| 4 |
��S�����B��A��D��MN?=S������B��A��D��C��?-S��MNC��=��
| 5 |
| 45 |
| 4 |
| 25 |
| 4 |
����������S��x�ĺ�����ϵʽΪ��
��0��t��
| 1 |
| 2 |
��
| 1 |
| 2 |
| 5 |
| 4 |
��1��t��
| 3 |
| 2 |
| 25 |
| 4 |
�����������Ƿdz����͵Ķ������ۺ��⣬ȫ�濼���˳�����ѧ�������εĶ����Ҫ֪ʶ�㣬���������κ�����ͼ�������ʡ�����ϵ���������ʽ���������뼸�α任��ƽ�ƣ������������ε��ж������ʡ�ȫ�������ε��ж������ʡ������ε����ʵȣ��ѵ����ڵڣ�3���ʣ�ʶ�������κ�������ƽ�ƹ��̵IJ�ͬ���ǹؼ����ڣ���Ϊ�п�ѹ���⣬�����漰�����ڶ࣬���㸴�ӣ�����ѶȺܴԿ����ۺ�����Ҫ��ܸߣ����кܺõ����ֶȣ�

��ϰ��ϵ�д�
�����Ŀ