题目内容
若抛物线y=ax2+bx+c的开口向上，且经过原点，请写出符合上述条件的一个解析式
y=x2
y=x2
．分析：根据二次函数的图象开口向上知道a＞0，又二次函数的图象过原点，可以得到c=0，所以解析式满足a＞0，c=0即可．
解答：解：∵抛物线y=ax2+bx+c的开口向上，且经过原点，
∴a＞0，c=0，
满足条件的解析式不唯一，
如当a=1，b=0，c=0，
即y=x2，
故答案为y=x2．
∴a＞0，c=0，
满足条件的解析式不唯一，
如当a=1，b=0，c=0，
即y=x2，
故答案为y=x2．
点评：本题主要考查二次函数的性质的知识点，此题是开放性试题，考查函数图形及性质的综合运用，对考查学生所学函数的深入理解、掌握程度具有积极的意义，但此题若想答对需要满足所有条件，如果学生没有注意某一个条件就容易错．本题的结论是不唯一的，其解答思路渗透了数形结合的数学思想．
练习册系列答案
相关题目
．问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（2013•镇江模拟）已知抛物线y=ax2+bx经过点A（-3，-3）和点P（t，0），且t≠0．
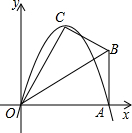
（2013•平谷区一模）如图，在直角坐标系中，已知直线