题目内容
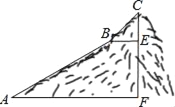
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF(结果保留根式).
【答案】(1) 400米;(2) (100![]() +400)米
+400)米
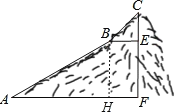
【解析】(1)作BH⊥AF于H,如图,在Rt△ABF中根据正弦的定义可计算出BH的长,从而得到EF的长;
(2)先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
试题解析:(1)作BH⊥AF于H,如图,
在Rt△ABH中,∵sin∠BAH=![]() ,
,
∴BH=800sin30°=400,
∴EF=BH=400米.
答:AB段山坡的高度EF为400米;
(2)在Rt△CBE中,∵sin∠CBE=![]() ,
,
∴CE=200sin45°=100![]() ,
,
∴CF=CE+EF=(100![]() +400)(米).
+400)(米).
答:山峰的高度CF为(100![]() +400)米.
+400)米.

练习册系列答案
相关题目
【题目】为弘扬“雷锋精神”,我县开展“做雷锋精神种子.当四品八德少年”主题征文比赛,已知每篇参赛征文成绩记![]() 分(
分(![]() ) ,组委会从
) ,组委会从![]() 篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
县主题征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
县主题征文比赛成绩频数分布直方图
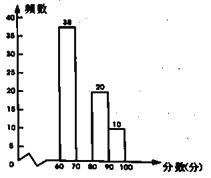
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)补全征文比赛成绩频数分布直方图:
(3)若![]() 分以上(含
分以上(含![]() 分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.