题目内容
【题目】【阅读学习】 刘老师提出这样一个问题:已知α为锐角,且tanα=![]() ,求sin2α的值.
,求sin2α的值.
小娟是这样解决的:
如图1,在⊙O中,AB是直径,点C在⊙O上,∠BAC=α,所以∠ACB=90°,tanα=![]() =
=![]() .
.
易得∠BOC=2α.设BC=x,则AC=3x,则AB=![]() x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α=
x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α=![]() = .
= .
【问题解决】
已知,如图2,点M、N、P为圆O上的三点,且∠P=β,tanβ =![]() ,求sin2β的值.
,求sin2β的值.


【答案】CD=![]() ;sin2α=
;sin2α=![]() ;
;![]() .
.
【解析】试题分析:(1)、根据题意的方法得出CD和sin2α的值;(2)、连接NO,并延长交⊙O于Q,连接MQ,MO,作MH⊥NO于H,设MN=k,则MQ=2k,NQ=![]() k,OM=
k,OM=![]() k,根据等面积法求出MH的长度,然后根据Rt△MHO计算三角函数的值.
k,根据等面积法求出MH的长度,然后根据Rt△MHO计算三角函数的值.
试题解析:(1)、![]() . sin2α=
. sin2α=![]() =
=![]() .
.
(2)、如图,连接NO,并延长交⊙O于Q,连接MQ,MO,作MH⊥NO于H.
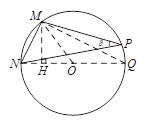
在⊙O中,∠NMQ=90°.
∵∠Q=∠P=β,OM=ON,
∴ ∠MON=2∠Q=2β
∵ tanβ=![]() ,
,
∴设MN=k,则MQ=2k,
∴NQ=![]() .
.
∴OM=![]() NQ=
NQ=![]() .
.
∵![]() ,
,
∴![]() .
.
∴ MH=![]() .
.
在Rt△MHO中,sin2β=sin∠MON =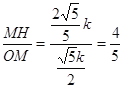 .
.

练习册系列答案
相关题目