题目内容
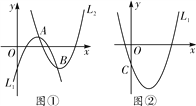
【题目】如图①，若抛物线L1的顶点A在抛物线L2上，抛物线L2的顶点B在抛物线L1上(点A与点B不重合)，我们把这样的两抛物线L1、L2称为“伴随抛物线”，可见一条抛物线的“伴随抛物线”可以有多条．
(1)抛物线L1：y＝－x2＋4x－3与抛物线L2是“伴随抛物线”，且抛物线L2的顶点B的横坐标为4，求抛物线L2的表达式；
(2)若抛物线y＝a1(x－m)2＋n的任意一条“伴随抛物线”的表达式为y＝a2(x－h)2＋k，请写出a1与a2的关系式，并说明理由；
(3)在图②中，已知抛物线L1：y＝mx2－2mx－3m(m>0)与y轴相交于点C，它的一条“伴随抛物线”为L2，抛物线L2与y轴相交于点D，若CD＝4m，求抛物线L2的对称轴．
【答案】（1）y＝(x－4)2－3（2）伴随抛物线的顶点不重合，∴m≠h，∴a1＝－a2（3）抛物线L2的对称轴为x＝±2.
【解析】试题分析：（1）先分别求得点A、点B的坐标，然后再利用待定系数法进行求解即可；
（2）根据：抛物线L1的顶点A在抛物线L2上，抛物线L2的顶点B也在抛物线L1上，可以列出两个方程，相加可得：（a1+a2 ）（m-h）2=0，可得a1=-a2；
（3）易得抛物线L1的顶点坐标为(1，－4m)，设抛物线L2的顶点的横坐标为h，则其纵坐标为mh2－2mh－3m，则有抛物线L2的表达式为y＝－mx2＋2mhx－2mh－3m，从而得点D的坐标为(0，－2mh－3m)，再根据点C的坐标为(0，－3m)，从而可得|(－2mh－3m)－(－3m)|＝4m，解得h＝±2，从而得抛物线L2的对称轴为x＝±2.
试题解析：(1)由y＝－x2＋4x－3可得A的坐标为(2，1)，
将x＝4代入y＝－x2＋4x－3，得y＝－3，∴B的坐标为(4，－3)，
设抛物线L2的解析式为y＝a(x－4)2－3； 将(2，1)代入y＝a(x－4)2－3，
得1＝a(2－4)2－3，解得a＝1，
∴抛物线L2的表达式为y＝(x－4)2－3；
(2)a1＝－a2，理由如下：
∵抛物线L1的顶点A在抛物线L2上，抛物线L2的顶点B在抛物线L1上，
∴可列方程组：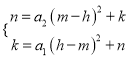 
，
整理，得(a1＋a2)(m－h)2＝0，
∵伴随抛物线的顶点不重合，∴m≠h，∴a1＝－a2；
(3)抛物线L1：y＝mx2－2mx－3m的顶点坐标为(1，－4m)，
设抛物线L2的顶点的横坐标为h，则其纵坐标为mh2－2mh－3m，
∴抛物线L2的表达式为y＝－m(x－h)2＋mh2－2mh－3m，
化简得，y＝－mx2＋2mhx－2mh－3m，
所以点D的坐标为(0，－2mh－3m)，
又点C的坐标为(0，－3m)，
可得|(－2mh－3m)－(－3m)|＝4m， 解得h＝±2，
∴抛物线L2的对称轴为x＝±2.
