题目内容
【题目】已知抛物线y=ax2﹣2ax﹣3a与y轴交于C点,交x轴于A、B,且OB=OC.
(1)求抛物线的解析式;
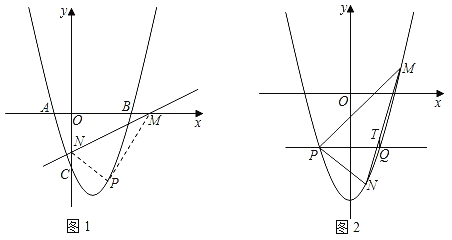
(2)如图1,直线l:y=![]() x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
(3)如图2,将原抛物线向左平移1个单位,向下平移t个单位,得到新抛物线C1.若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m翻折交新抛物线C1于N,过Q作QT∥y轴,交MN于点T,求![]() 的值.
的值.
【答案】(1)抛物线的表达式为y=x2﹣2x﹣3;(2)直线l的表达式为:y=![]() x﹣
x﹣![]() ;(3)1.
;(3)1.
【解析】
(1)OB=OC=3a,故点B(3a,0),将点B的坐标代入y=ax22ax3a,即可求解;
(2)求出点P的坐标(﹣![]() b,
b,![]() b),将点P的坐标代入抛物线表达式,即可求解;
b),将点P的坐标代入抛物线表达式,即可求解;
(3)计算xP+xM=k,同理可得:xP+xN=﹣k,而xT=xQ=﹣xP,而TH∥MG,故![]() ,即
,即![]() =
=![]() =1.
=1.
解:(1)∵c=﹣3a,
∴OB=OC=3a,故点B(3a,0),
将点B的坐标代入y=ax2﹣2ax﹣3a并解得:a=1或﹣![]() (舍去﹣
(舍去﹣![]() ),
),
故抛物线的表达式为:y=x2﹣2x﹣3;

(2)连接OP,交MN于点K,则OP⊥MN,
则直线OP的表达式为:y=﹣2x,而直线MN的表达式为:y=![]() x+b,
x+b,
联立上述两个表达式并解得:x=﹣![]() b,则点K(﹣
b,则点K(﹣![]() b,
b,![]() b),
b),
∵点K是OP的中点,由中点公式得:点P的坐标为(﹣![]() b,
b,![]() b),
b),
将点P的坐标代入抛物线表达式得:(﹣![]() b)2﹣2(﹣
b)2﹣2(﹣![]() b)﹣3=
b)﹣3=![]() b,解得:b=﹣
b,解得:b=﹣![]()
(不合题意值已舍去);
故直线l的表达式为: y=![]() x﹣
x﹣![]() ;
;
(3)平移后抛物线的表达式C1:y=x2﹣4﹣t①,
设直线PM的表达式为:y=kx+c②;则PN的表达式为:y=﹣kx+d,
联立①②并整理得:x2﹣kx﹣(4+t+c)=0,
∴xP+xM=k,
同理可得:xP+xN=﹣k,而xT=xQ=﹣xP,
如图2,过点N作x轴的平行线交过点M与y轴的平行线于点G,延长TQ交NG于点H,

∴TH∥MG,故![]() ,即
,即![]() =
=![]() =1.
=1.

 阅读快车系列答案
阅读快车系列答案

