题目内容
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
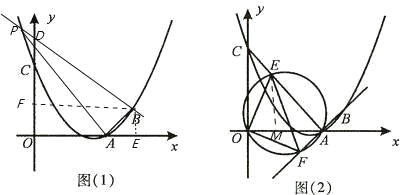
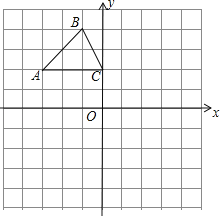
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.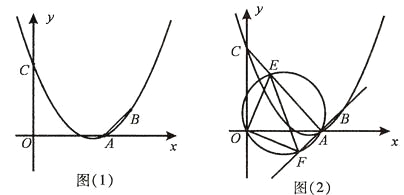
【答案】:(1)(0,3);
(2)点P的坐标为:(﹣1,6),(4,﹣1),(0,3);
(3)E点坐标为![]() .
.
【解析】
(1)根据A(3,0),B(4,1)两点利用待定系数法求二次函数解析式;
(2)从当△PAB是以AB为直角边的直角三角形,且∠PAB=90°与当△PAB是以AB为直角边的直角三角形,且∠PBA=90°,分别求出符合要求的答案;
(3)根据当OE∥AB时,△FEO面积最小,得出OM=ME,求出即可.
解:(1)∵抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,
∴![]() ,
,
解得: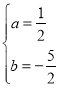 ,
,
∴![]() ;
;
∴点C的坐标为:(0,3);
(2)当△PAB是以AB为直角边的直角三角形,且∠PAB=90°,
∵A(3,0),B(4,1),
∴AM=BM=1,
∴∠BAM=45°,
∴∠DAO=45°,
∴AO=DO,
∵A点坐标为(3,0),
∴D点的坐标为:(0,3),
∴直线AD解析式为:y=kx+b,将A,D分别代入得:
∴0=3k+b,b=3,
∴k=﹣1,
∴y=﹣x+3,
∴![]() ,
,
∴x2﹣3x=0,
解得:x=0或3,
∴y=3或0(不合题意舍去),
∴P点坐标为(0,3),
当△PAB是以AB为直角边的直角三角形,且∠PBA=90°,
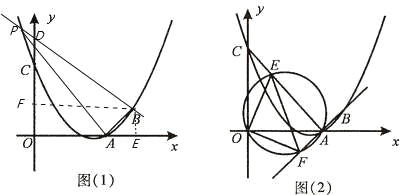
由(1)得,FB=4,∠FBA=45°,
∴∠DBF=45°,∴DF=4,
∴D点坐标为:(0,5),B点坐标为:(4,1),
∴直线AD解析式为:y=kx+b,将B,D分别代入得:
∴1=4k+b,b=5,
∴k=﹣1,
∴y=﹣x+5,
∴![]() ,
,
∴x2﹣3x﹣4=0,
解得:x1=﹣1,x2=4,
∴y1=6,y2=1,
∴P点坐标为(﹣1,6),(4,﹣1)
∵P(4,﹣1)与点B重合,故舍去
∴点P的坐标为:(﹣1,6),(0,3);
(3)作EM⊥BO,
∵当OE∥AB时,△FEO面积最小,
∴∠EOM=45°,
∴MO=EM,
∵E在直线CA上,
∴E点坐标为(x,﹣x+3),
∴x=﹣x+3,
解得:![]() ,
,
∴E点坐标为![]() .
.