Question

【题目】某校创建“环保示范学校”，为了解全校学生参加环保类社团的意愿，在全校随机抽取了50名学生进行问卷调查．问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团，也可以不选)，对选择了社团的学生的问卷情况进行了统计，如下表：

社团名称	A 酵素制作社团	B 回收材料小制作社团	C 垃圾分类社团	D 环保义工社团	E 绿植养护社团
人数	10	15	5	10	5

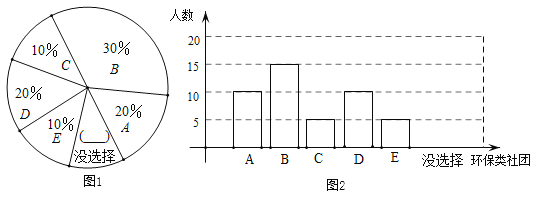
（1）根据以上信息填空：这5个数的中位数是______；扇形图中没选择的百分比为______；

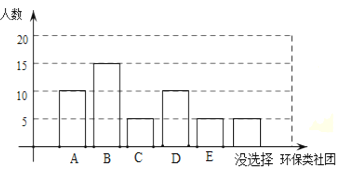
（2）①补全条形统计图；②若该校有1400名学生，根据调查统计情况，请估计全校有多少学生愿意参加环保义工社团；

（3）若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加，请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率．

Answer 1

【答案】（1）10，10%；（2）①见解析，②全校约有280名学生愿意参加环保义工社团；（3）见解析，.

【解析】

对于（1），根据中位数的定义得到答案，利用各部分所占的百分比之和为1求出没有选择的百分比,

对于（2），①由（1）即可补全条形统计图，②利用样本估计总体的思想解决问题即可；

对于（3），画出树状图将所有可能出现的情况表示出来，再找出这两名同学同时选择绿植养护社团的情况，根据概率的公式得到答案.

解：（1）这5个数从小到大排列：5，5，10，10，15，故中位数为10．

没有选择的占1-10%-30%-20%-10%-20%=10%

故答案为：10；10%

（2）①补全条形图如下：②1400×20%=280（名），∴全校约有280名学生愿意参加环保义工社团；

（3）酵素制作社团、绿植养护社团分别用A、B表示，画树状图如下：

由树状图知共有4种等可能结果，其中两人同时选择绿植养护社团只有一种情况，∴两人同时选择绿植养护社团的概率为．