题目内容
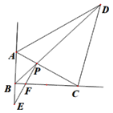
【题目】已知:BF为△ABC的外角∠ABE的平分线,D为BF上一点,且AD=CD.
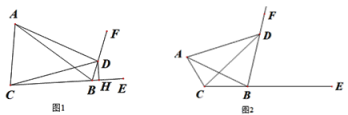
(1)如图1,过点D作DH⊥CE于点H,若AB=8,BC=6,求BH的长.
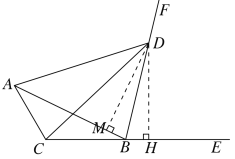
(2)如图2,若∠ABC=24°,∠ABD=78°,∠BAD=60°,求∠BAC的度数.
【答案】(1)BH=1;(2)∠BAC=48°.
【解析】
(1)过D作DM⊥AB于M,由角平分线上的点到角两边的距离相等可得DM=DH,利用HL即可判定Rt△ADM≌Rt△CDH,得到AM=CH,易证Rt△DBM≌Rt△DBH,得到BM=BH,然后利用AB=AM+BM,CH=BC+BH即可求出BH;
(2)过D作DH⊥CE于H,DM⊥AB于M,由角平分线的性质定理可得DM=DH,利用HL即可判定Rt△ADM≌Rt△CDH,得到∠DCH=∠BAD=60°,再根据等边对等角可得∠DAC=∠DCA,△ABC中,利用三角形内角和定理即可求出∠BAC.
解:(1)过D作DM⊥AB于M,如图所示,
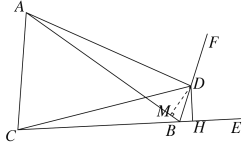
∵BF平分∠ABE,DH⊥CE,DM⊥AB,
∴DM=DH
在Rt△ADM和Rt△CDH中,
![]()
∴Rt△ADM≌Rt△CDH(HL)
∴AM=CH
在Rt△DBM和Rt△DBH中,
![]()
∴Rt△DBM≌Rt△DBH(HL)
∴BM=BH
又∵AB=AM+BM,CH=BC+BH
∴AB=BC+2BH
∴BH=![]()
(2)过D作DH⊥CE于H,DM⊥AB于M,
∵BF平分∠ABE,DH⊥CE,DM⊥AB,
∴DM=DH
在Rt△ADM和Rt△CDH中,
![]()
∴Rt△ADM≌Rt△CDH(HL)
∴∠DCH=∠BAD=60°
∵AD=CD
∴∠DAC=∠DCA
∴∠DCA=∠BAC+60°,
在△ABC中,∠BAC+∠ACB+∠ABC=180°,
即∠BAC+∠BAC+60°+∠ABC=180°
∴2∠BAC=180°-60°-24°=96°
∴∠BAC=48°.

 阅读快车系列答案
阅读快车系列答案