题目内容
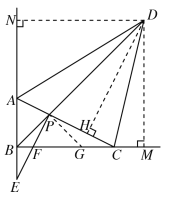
【题目】如图,在△ABC中,AB=2,BC=4,其两条外角平分线AD、CD交于点D,且∠ADC=45°,连接BD交AC于点P,过点P作PE⊥AC交BC于点F,交AB的延长线于点E.
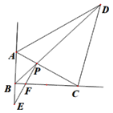
(1)求证:∠ABC=90° ;
(2)求S△PFC:S△PBF的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)设∠BAC=![]() ,∠ACB=
,∠ACB=![]() ,然后分别表示出∠DAC和∠DCA,利用三角形内角和可求出
,然后分别表示出∠DAC和∠DCA,利用三角形内角和可求出![]() ,即可得证;
,即可得证;
(2)由角平分线的性质易得BD平分∠ABC,过P作PG⊥BD,易证△PBE≌△PGC,然后证明△PCF≌△PEA,可得CF=AE,设BF=x,则CF=AE=4-x,可得BE=2-x,由BF与BE的比例关系可解出x,得到BF与FC的比例关系即为面积比.
解:(1)设∠BAC=![]() ,∠ACB=
,∠ACB=![]() ,
,
∵AD、CD为△ABC的外角平分线,
∴∠DAC=![]()
∠DCA=![]()
在△ACD中,∠DAC+∠ACD+∠ADC=180°,
即![]()
∴![]()
∴∠ABC=![]()
(2)如图所示,过D作DN⊥AB于点N,DM⊥BC于点M,DH⊥AC于点H,
∵AD平分∠CAN,CD平分∠ACM,
∴DN=DH,DH=DM
∴DN=DM
∴BD平分∠ABC
又∵∠ABC=90°,
∴∠PBC=45°,
过P作PG⊥PB,交BC于点G,如图,
∴∠PBG=∠PGB=45°
∴PB=PG
∵∠PCG+∠BAC=90°,∠E+∠BAC=90°
∴∠PCG=∠E
∵PE⊥AC
∴∠CPG+∠GPF=90°
又∵∠EPB+∠GPF=90°
∴∠CPG=∠EPB
在△PBE和△PGC中,
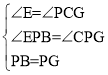
∴△PBE≌△PGC(AAS)
∴PE=PC
在△PCF和△PEA中,
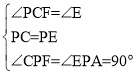
∴△PCF≌△PEA(ASA)
∴CF=AE
设BF=x,则CF=AE=4-x,BE=AE-AB=2-x,
∵∠ACB=∠E,∠ABC=∠FBE=90°,
∴△ABC∽△FBE
∴![]()
即![]() ,解得x=
,解得x=![]()
∴CF=![]()
∴![]()
即S△PFC:S△PBF的值为![]() .
.

 阅读快车系列答案
阅读快车系列答案