题目内容
【题目】如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.

(1)点E在整个运动过程中,试说明总有:CE=EF;
(2)求y与x之间关系的表达式,并写出x的取值范围.
【答案】(1)见解析;(2)y=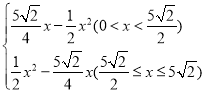
【解析】
(1)分两种情况:点F在BC的延长线上和在BC边上,在BC的延长线上时,作辅助线,构建三角形全等,证明△AEM≌△EFN和△ADE≌△CDE(SAS),可得AE=CE=EF;在BC边上时,同理可证明∠BAE=∠CFE,再证明△BEA≌△BEC得∠BAE=∠BCE,所以∠CFE=∠FCE,故可得结论;
(2)分两种情况:根据三角形的面积公式可得y与x之间关系的函数表达式,根据勾股定理计算BD的长可得x的取值.
(1)证明:如图1,过E作MN∥AB,交AD于M,交BC于N,
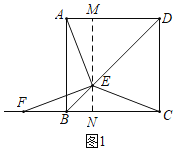
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
如图2,同理可证明∠BAE=∠CFE,

∵BD是正方形ABCD的对角线,
∴∠ABE=∠CBE=45°
又AB=CB,BE=BE
∴△BEA≌△BEC
∴∠BAE=∠BCE
∴∠CFE=∠FCE
∴CE=FE
因此,点E在整个运动过程中,总有:CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:![]() ,
,
∴![]() ,
,
由题意得:BE=2x,
∴![]() ,
,
由(1)知:AE=EF=EC,
分两种情况:
①当![]() 时,如图3,
时,如图3,
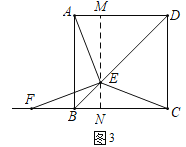
∵AB=MN=10,
∴ME=FN=10-![]() x,
x,
∴BF=FN-BN=10-![]() x-
x-![]() x=10-2
x=10-2![]() x,
x,
∴![]() ;
;
②当![]() 时,如图4,过E作EN⊥BC于N,
时,如图4,过E作EN⊥BC于N,
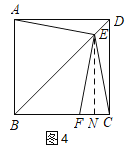
∴EN=BN=![]() x,
x,
∴FN=CN=10-![]() x,
x,
∴BF=BC-2CN=10-2(10-![]() x)=2
x)=2![]() x-10,
x-10,
∴![]() ;
;
综上,y与x之间关系的函数表达式为: y=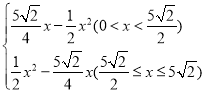

【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
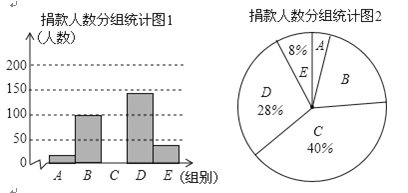
被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?





