题目内容
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.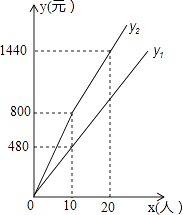
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
【答案】
(1)6;8
(2)
解:设y1=k1x,
![]() 函数图像经过点(0,0)和(10,480),
函数图像经过点(0,0)和(10,480),
![]() 10k1=480,
10k1=480,
![]() k1=48,
k1=48,
![]() y1=48x;
y1=48x;
0≤x≤10时,设y2=k2x,
![]() 函数图像经过点(0,0)和(10,800),
函数图像经过点(0,0)和(10,800),
![]() 10k2=800,
10k2=800,
![]() k2=80,
k2=80,
![]() y2=80x,
y2=80x,
x>10时,设y2=kx+b,
![]() 函数图像经过点(10,800)和(20,1440),
函数图像经过点(10,800)和(20,1440),
![]()
![]() ,
,
![]()
![]() ,
,
![]() y2=64x+160;
y2=64x+160;
![]() y2=
y2= ![]() ;
;
(3)
解:设A团有n人,则B团的人数为(50﹣n),
当0<50-n≤10时,即40≤n≤50,则48n+80(50﹣n)=3040,
解得n=30(不符合题意舍去),
当10<50-n<50时,即0<n<40,则48n+64(50﹣n)+160=3040,
解得n=20,
则50﹣n=50﹣20=30.
答:A团有20人,B团有30人.
【解析】解:(1)由y1 图像上点(10,480),得到10人的费用为480元,![]() a=
a= ![]() ×10=6;
×10=6;
由y2 图像上点(10,800)和(20,1440),得到20人中后10人费用为640元,
∴b= ![]() ×10=8;
×10=8;

练习册系列答案
相关题目





