题目内容
【题目】如图，抛物线y=﹣x2+6x与x轴交于O，A两点，与直线y=2x交于O，B两点．点P在线段OA上以每秒1个单位的速度从点O向终点A运动，作EP⊥x轴交直线OB于E；同时在线段OA上有另一个动点Q，以每秒1个单位的速度从点A向点O运动（不与点O重合）．作CQ⊥x轴交抛物线于点C，以线段CQ为斜边作如图所示的等腰直角△CQD．设运动时间为t秒．
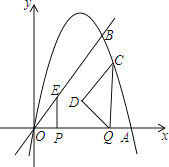
（1）求点B的坐标；
（2）当t=1秒时，求CQ的长；
（3）求t为何值时，点E恰好落在△CQD的某一边所在的直线上．
【答案】（1）（4，8）．（2）CQ的长为5．（3）当t=1.5或3﹣
或3或3+时，点E恰好落在△CQD的某一边所在的直线上．
【解析】
试题分析：（1）由抛物线与直线相交，联立找出关于x的一元二次方程，解方程即可得出结论；
（2）找出当t=1时，C点的横坐标，代入抛物线即可得出C点的纵坐标，C点的纵坐标的绝对值即CQ的长度；
（3）用t表示出E点的坐标，以及线段DQ、CD、CQ所在的直线解析式，由点在直线上，即可解出t的值．
解：（1）∵抛物线y=﹣x2+6x与与直线y=2x交于O，B两点，
∴2x=﹣x2+6x，解得：x=0（舍去），x=4，
当x=4时，y=2×4=8．
故点B的坐标为（4，8）．
（2）∵抛物线y=﹣x2+6x与x轴交于O，A两点，
∴﹣x2+6x=0，解得：x=0（舍去），x=6，
即点A的坐标为（6，0）．
当t=1时，点C横坐标x=6﹣1=5，
点C纵坐标y=﹣52+5×6=5．
故点C坐标为（5，5），
即当t=1秒时，CQ的长为5．
（3）过点D作DF⊥CQ于点F，如图所示．
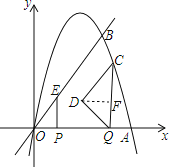
当时间为t时，E点坐标为（t，2t），C点坐标为（6﹣t，6t﹣t2）．
∵△CQD为等腰直角三角形，且CQ⊥x轴，
∴DF∥x轴，且∠CDF=∠QDF=45°，
∴Q点坐标为（6﹣t，0），
设CD所在的直线解析式为y=x+b1，DQ所在的直线解析式为y=﹣x+b2．
结合C、Q点的坐标可知：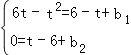
，
解得：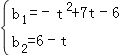
．
故CD所在直线的解析式为y=x﹣t2+7t﹣6，DQ所在的直线解析式为y=﹣x﹣t+6，
而CQ所在直线的解析式为x=6﹣t．
当点E在CD所在的直线上时，有2t=t﹣t2+7t﹣6，
解得：t=3±；
当点E在DQ所在的直线上时，有2t=﹣t﹣t+6，
解得：t=1.5；
当点E在CQ所在的直线上时，有t=6﹣t，
解得：t=3．
综上可知：当t=1.5或3﹣或3或3+时，点E恰好落在△CQD的某一边所在的直线上．
