题目内容
同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是
| A.a∥b | B.b⊥d | C.a⊥d | D.b∥c |
C
试题分析:由a⊥b,b⊥c,c⊥d,可知A、D选项是错误的,可排除。由于这四条线是在同一平面,所以b⊥c,c⊥d 可以推出b∥d, a⊥b,b⊥c,可以推出a∥c,而c⊥d可以推出a⊥d
点评:本题考查的是同意平面内各条直线之间的相互关系,若直线a与直线b互相垂直,直线b与直线c互相垂直,则直线a与直线b互相平行;若直线a与直线b互相垂直,直线b与直线c互相垂直,则直线a与直线c互相平行;若直线a与直线b互相平行,直线b与直线c互相平行,则直线a与直线c互相平行。

练习册系列答案
相关题目
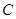 为线段
为线段 的中点,
的中点,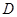 在线段
在线段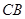 上,
上,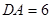 ,
,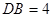 ,则
,则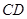 的长度是______.
的长度是______.