题目内容
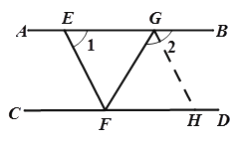
【题目】如图，直线AB，CD被直线EF所截，AB∥CD，FG平分∠EFD .
（1）若∠1=54° ，求∠2的度数（完成填空）.
解：（1）∵AB∥CD（已知）
∴∠ = 180 ° －∠1（ ）
∵ FG平分∠EFD，∠1=54°（已知）
∴∠GFD=
∠EFD = °
∵ AB∥CD
∴∠2 = － ∠GFD = ° （两直线平行，同旁内角互补）
（2）作∠FGB 的角平分线GH交CD于点H. 若GH∥EF 时，求∠1的度数.
【答案】（1）EFD ；两直线平行，同旁内角互补；63；180°；117 ；
（2）∠1 的度数为60 °
【解析】解：（1）∵AB∥CD（已知）
∴∠ EFD = 180 ° －∠1 （两直线平行，同旁内角互补）
∵ FG平分∠EFD，∠1=54°（已知）
∴∠GFD=
∠EFD = 63 °
∵ AB∥CD
∴∠2 = 180° － ∠GFD = 117 °（两直线平行，同旁内角互补）
（2）∵ GH平分∠BGF
∴∠FGH= ∠BGH
∵ EF∥GH
∴∠FGH= ∠EFG
∵ AB∥CD
∴∠EGF= ∠GFH
∵ FG平分∠EFD
∴∠EFG= ∠GFH
∴∠EGF= ∠GFH= ∠BGH=
° =60 °
∵ EF∥GH
∴∠1 =∠BGH= 60 °
练习册系列答案
相关题目
