题目内容
已知A，B，C是⊙O上不同的三个点，∠AOB=60°，则∠ACB=
- A.60°
- B.30°
- C.60°或120°
- D.30°或150°
D
分析：根据同弧所对的圆周角是所对的圆心角的一半即可求∠ACB的度数．
解答：
解：∵∠AOB=60°，
当点C在优弧上时，
∴∠ACB=
∠AOB=30°（同弧所对的圆周角是所对的圆心角的一半）；
当点C在劣弧上时，∠AC′B=180°-∠ACB=150°，
故选D．
点评：本题考查了圆周角定理的运用．一条弧所对的圆周角等于它所对的圆心角的一半．
分析：根据同弧所对的圆周角是所对的圆心角的一半即可求∠ACB的度数．
解答：
解：∵∠AOB=60°，当点C在优弧上时，
∴∠ACB=
∠AOB=30°（同弧所对的圆周角是所对的圆心角的一半）；当点C在劣弧上时，∠AC′B=180°-∠ACB=150°，
故选D．
点评：本题考查了圆周角定理的运用．一条弧所对的圆周角等于它所对的圆心角的一半．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
相关题目
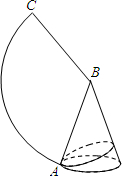如图是一个圆锥与其侧面展开图，已知圆锥的底面半径是2，母线长是6．
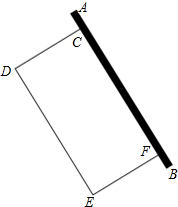米1.75元，建新围栏的价格是每米4.5元，设利用旧围栏CF的长度为x米，修建草坪围栏所需的总费用为y元．